
分析 根据二次根式的混合运算顺序,首先计算开方,然后计算乘法和除法,最后计算加法,求出算式$\sqrt{\frac{5(5a-{a}^{2})}{{b}^{2}+2}}$+$\frac{a\sqrt{a}+b\sqrt{b}}{a-b}$($\sqrt{\frac{2}{a}}$-$\sqrt{\frac{2}{b}}$)÷($\sqrt{a}$-$\frac{a+b}{\sqrt{b}}$)的值是多少即可.
解答 解:$\sqrt{\frac{5(5a-{a}^{2})}{{b}^{2}+2}}$+$\frac{a\sqrt{a}+b\sqrt{b}}{a-b}$($\sqrt{\frac{2}{a}}$-$\sqrt{\frac{2}{b}}$)÷($\sqrt{a}$-$\frac{a+b}{\sqrt{b}}$)
=$\sqrt{\frac{5×2}{5b}}$+$\frac{(\sqrt{a}+\sqrt{b})(a-\sqrt{ab}+b)}{a-b}$×$\frac{\sqrt{2}(\sqrt{a}-\sqrt{b})}{\sqrt{ab}}$×$\frac{\sqrt{b}}{\sqrt{ab}-(a+b)}$
=$\sqrt{\frac{2}{b}}+\frac{\sqrt{2}}{\sqrt{a}}$
=$\frac{\sqrt{2}(\sqrt{a}+\sqrt{b})}{\sqrt{ab}}$
=$\sqrt{a}+\sqrt{b}$
=$\sqrt{{(\sqrt{a}+\sqrt{b})}^{2}}$
=$\sqrt{a+b+2\sqrt{ab}}$
=$\sqrt{5+2\sqrt{2}}$.
点评 此题主要考查了二次根式的混合运算,要熟练掌握,解答此题的关键是要明确:①与有理数的混合运算一致,运算顺序先乘方再乘除,最后加减,有括号的先算括号里面的.②在运算中每个根式可以看做是一个“单项式”,多个不同类的二次根式的和可以看作“多项式”.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:选择题
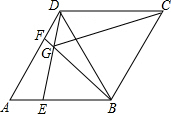 如图:△ABC是等边三角形,以BD为边向外作等边三角形△DBC,点E,F分别在AB,AD上且AE=DF,连接BF,DE,两直线相交于点G,连接CG,下列结论:①∠BGE=60°,②CG平分∠BGD,③CG=DG+BG.其中正确的是( )
如图:△ABC是等边三角形,以BD为边向外作等边三角形△DBC,点E,F分别在AB,AD上且AE=DF,连接BF,DE,两直线相交于点G,连接CG,下列结论:①∠BGE=60°,②CG平分∠BGD,③CG=DG+BG.其中正确的是( )| A. | 仅有①③ | B. | 仅有①② | C. | 仅有②③ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com