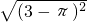练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    数学公式=________；|数学公式-3|=________．

    π-3    3-
    分析：根据算术平方根和绝对值的定义，解答即可
    解答：∵3-π＜0，
    ∴=π-3，
    ∵-3＜0，
    ∴|-3|=3-．
    点评：本题主要考查了算术平方根和绝对值的定义，注意一个数的算术平方根是非负数，以及先确定绝对值符号中代数式的正负再去绝对值符号．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    已知点P（-1，-2）是反比例函数图象上的一点，则这个反比例函数的解析式是________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

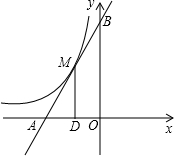    如图，直线y=k1x+b与双曲线数学公式只有一个交点M（-2，4），且直线与x轴、y轴分别交于A、B两点，MD垂直平分线段OA，垂足为D，试分别求出直线和双曲线所对应的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

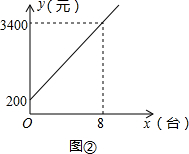    受西南地区旱情影响，某山区学校学生缺少饮用水．我市中小学生决定捐出自己的零花钱，购买300吨矿泉水送往灾区学校．运输公司听说此事后，决定免费将这批矿泉水送往灾区学校．公司现有大、中、小三种型号货车．各种型号货车载重量和运费如表①所示．
    大中 小
    载重（吨/台） 20 15 12
    运费（元/辆）150012001000
    司机及领队往返途中的生活费y（单位：元）与货车台数x（单位：台）的关系如图②所示．为此，公司支付领队和司机的生活费共8200元．
    （1）求出y与x之间的函数关系式及公司派出货车的台数；
    （2）设大型货车m台，中型货车n台，小型货车p台，且三种货车总载重量恰好为300吨．设总运费为W（元），求W与小型货车台数P之间的函数关系式．（不写自变量取值范围）；
    （3）若本次派出的货车每种型号不少于3台且各车均满载．
    ①求出大、中、小型货车各多少台时总运费最少及最少运费？
    ②由于油价上涨，大、中、小三种型号货车的运费分别增加500元/辆、300元/辆、a元/辆，公司又将如何安排，才能使总运费最少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

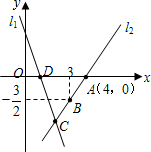    如图，直线l1的解析表达式为：y=-3x+3，且l1与x轴交于点D，直线l2经过点A，B，直线l1，l2交于点C．
    （1）求直线l2的函数关系式；
    （2）求△ADC的面积；
    （3）若点H为坐标平面内任意一点，在坐标平面内是否存在这样的点H，使以A、D、C、H为顶点的四边形是平行四边形？若存在，请直接写出点H的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，在梯形ABCD中，AD∥BC，∠A=90°，AB=7，AD=2，BC=3．问：线段AB上是否存在点P，使得以P、A、D为顶点的三角形与以P、B、C为顶点的三角形相似？若存在，这样的总共有几个？并求出AP的长；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    按要求作图：已知△ABC，作出AC　BC边上的高和中线．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    （1）如图1，已知△ABC中，∠C=90°，AC=BC，点C在直线l上，过点A作AE⊥l于E，BF⊥l于F，则线段CE与BF的数量关系是______；
    （2）如图2，分别以AB、AC为一边向△ABC外作正方形ABGE和ACHF，直线AN⊥BC于N，若EP⊥AN于P，FQ⊥AN于Q，判断线段EP、FQ之间的数量关系，并说明；
    （3）如图3，分别以AB、AC为一边向△ABC外作矩形ABGE和ACHF，线AN⊥BC于N，若EP⊥AN于P，FQ⊥AN于Q，如果GB=kAB，HC=kAC，（2）中结论还成立吗？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    数学公式．

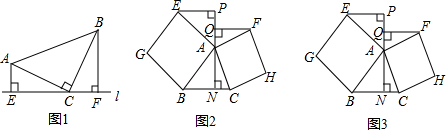
    查看答案和解析>>

    同步练习册答案