练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
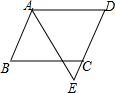
    10．如图，在?ABCD中，AB=6，AD=9，∠BAD的平分线交DC的延长线于点E，CE的长为（　　）
    A．2B．3C．4D．2.5

    分析 利用平行四边形的性质以及平行线的性质得出∠BAF=∠BFA=∠CFE=∠E，进而得出AB=BF，CE=CF，即可得出答案．

    解答 解：∵?ABCD中，
    ∴BC=AD=9，AD∥BC，AB∥DE，
    ∴∠DAF=∠BFA，∠BAF=∠E，
    ∵∠BAF=∠DAF，
    ∴∠BAF=∠BFA=∠CFE=∠E，
    ∴AB=BF=6，CE=CF，
    ∴FC=3，
    ∴CE=3，
    故选B．

    点评 此题主要考查了平行四边形的性质以及平行线的性质等知识，熟练应用平行四边形的性质得出是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    20．已知三条直线L1：（m-2）x-y=1、L2：x-y=3、L3：2x-y=2相交于同一点，则m=（　　）
    A．6B．5C．4D．-3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．如图，直线m的表达式为y=-3x+3，且与x轴交于点B，直线n经过点A（4，0），且与直线m交于点C（t，-3）
    （1）求直线n的表达式．
    （2）求△ABC的面积．
    （3）在直线n上存在异于点C的另一点P，使△ABP与△ABC的面积相等，请直接写出点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．已知一组数据2，a，4，5的众数是5，则这组数据的平均数为4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．在矩形ABCD中，已知AB=2，BC=4，对角线AC的垂直平分线分别交AD、AC于点E、O，连接CE，求CE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．当x=1时，分式$\frac{x+2m}{x-n}$无意义；当x=4时分式的值为0，则（m+n）2012的值是1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．若m＜n，则下列各式正确的是（　　）
    A．2m＞2nB．m-2＞n-2C．-3m＞-3nD．$\frac{m}{3}$＞$\frac{n}{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．在日常生活中如取款、上网都需要密码，有一种用“因式分解法”产生的密码方便记忆，例如，对于多项式x4-y4，因式分解的结果是（x-y）（x+y）（x2+y2）．若取x=9，y=9时，则各个因式的值为（x-y）=0，（x+y）=18，（x2+y2）=162，于是就可以把“018162”作为一个六位数的密码，对于多项式x3-xy2，取x=20，y=10，用上述方法产生的密码不可能是（　　）
    A．201030B．201010C．301020D．203010

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．已知A、B两地的路程为240千米，某经销商每天都要用汽车或火车将x吨保鲜品一次性由A地运往B地，受各种因素限制，下一周只能采用汽车或火车中的一种进行运输，且须提前预订，现有货运收费项目及收费村准表、行驶路程s（千米）与行驶时间t（时）的函数图象（如图1）、上周货运量折线统计图（如图2）等信息如下：

    货运收费项目及收费标准表
    运输工具运输费单价：元/（吨•千米）冷藏费单价：元/（吨•时）固定费用：元/次
    汽车25200
    火车1.652280
    （1）汽车的速度为60千米/时，火车的速度为100千米/时；
    （2）设每于用汽车和火车运输的总费用分别为y汽（元）和y火（元），分别求y汽、y火与x的函数关系式（不必写出x的取值范围），及x为何值时y汽＞y火（总费用=运输费+冷藏费+固定费用）；
    （3）根据上周货运量的折线统计图，请你从平均数和折线图走势两个角度分析，建议该经销商应提前为下周预定哪种运输工具，才能使每天的运输总费用较省？

    查看答案和解析>>

    同步练习册答案