
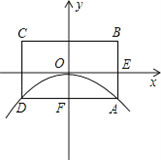
解:(1)∵抛物线的顶点为坐标原点,
∴A、D关于抛物线的对称轴对称;
∵E是AB的中点,
∴O是矩形ABCD对角线的交点,又B(2,1)
∴A(2,﹣1)、D(﹣2,﹣1);
由于抛物线的顶点为(0,0),可设其解析式为:y=ax2,
则有:4a=﹣1,a=﹣
∴抛物线的解析式为:y=﹣ x2.
x2.
(2)①证明:由抛物线的解析式知:P(a,﹣ a2),而R(a,1)、F(0,﹣1),
a2),而R(a,1)、F(0,﹣1),
则:PF=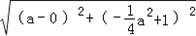 =
=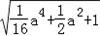 =
= a2+1,
a2+1,
PR=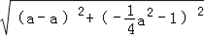 =
= a2+1.
a2+1.
∴PF=PR.
②由①得:RF=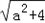 ;若△PFR为等边三角形,
;若△PFR为等边三角形,
则RF=PF=PR,得: =
= a2+1,
a2+1,
即: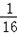 a4﹣
a4﹣ a2﹣3=0,得:a2=﹣4(舍去),a2=12;
a2﹣3=0,得:a2=﹣4(舍去),a2=12;
∴a=±2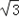 ,﹣
,﹣ a2=﹣3;
a2=﹣3;
∴存在符合条件的P点,坐标为(2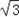 ,﹣3)、(﹣2
,﹣3)、(﹣2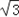 ,3).
,3).
③同①可证得:QF=QS;在等腰△SQF中,∠1= (180°﹣∠SQF);
(180°﹣∠SQF);
同理,在等腰RPF中,∠2= (180°﹣∠RPF);
(180°﹣∠RPF);
∵QS⊥BC、PR⊥BC,
∴QS∥PR,∠SQP+∠RPF=180°
∴∠1+∠2= (360°﹣∠SQF﹣∠RPF)=90°
(360°﹣∠SQF﹣∠RPF)=90°
∴∠SFR=180°﹣∠1﹣∠2=90°,即△SFR是直角三角形.


科目:初中数学 来源: 题型:
 如图所示,已知抛物线y=x2-1与x轴交于A、B两点,与y轴交于点C.
如图所示,已知抛物线y=x2-1与x轴交于A、B两点,与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:
 BC交抛物线于点P.
BC交抛物线于点P.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,已知抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),抛物线的对称轴x=2交x轴于点E.
如图所示,已知抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),抛物线的对称轴x=2交x轴于点E.查看答案和解析>>
科目:初中数学 来源: 题型:
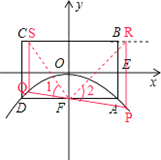
 (2012•衡阳)如图所示,已知抛物线的顶点为坐标原点O,矩形ABCD的顶点A,D在抛物线上,且AD平行x轴,交y轴于点F,AB的中点E在x轴上,B点的坐标为(2,1),点P(a,b)在抛物线上运动.(点P异于点O)
(2012•衡阳)如图所示,已知抛物线的顶点为坐标原点O,矩形ABCD的顶点A,D在抛物线上,且AD平行x轴,交y轴于点F,AB的中点E在x轴上,B点的坐标为(2,1),点P(a,b)在抛物线上运动.(点P异于点O)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com