
分析 (1)利用二次根式的性质得原式=$\sqrt{{5}^{2}}$•$\sqrt{0.4}$,然后利用二次根式的乘法法则运算;
(2)利用二次根式的性质得原式=-$\sqrt{{7}^{2}×\frac{1}{7}}$,然后利用二次根式的乘法法则运算;
(3)利用二次根式的性质得原式=$\sqrt{(-2m)^{2}•(-\frac{1}{2m})}$,然后利用二次根式的乘法法则运算.
解答 解:(1)原式=$\sqrt{{5}^{2}}$•$\sqrt{0.4}$=$\sqrt{25×0.4}$=$\sqrt{10}$;
(2)原式=-$\sqrt{{7}^{2}×\frac{1}{7}}$=-$\sqrt{7}$;
(3)原式=$\sqrt{(-2m)^{2}•(-\frac{1}{2m})}$=$\sqrt{-2m}$.
点评 本题考查了二次根式的性质与化简:熟练掌握二次函数的性质.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.
如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
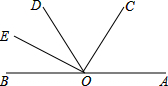 如图,已知AOB是一条直线,OC是∠AOD 的平分线,OE是∠BOD的平分线.
如图,已知AOB是一条直线,OC是∠AOD 的平分线,OE是∠BOD的平分线.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ${3^{-2}}=-\frac{1}{9}$ | B. | ${(-3)^{-2}}=-\frac{1}{9}$ | C. | ${(-\frac{1}{3})^{-2}}=9$ | D. | ${(-\frac{1}{3})^{-2}}=-9$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
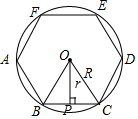 三正多边形的中心、半径、中心角、弦心距、边长之间的关系如图:请指出圆内接正六边形的中心、半径、中心角、弦心距.若设半径为R、弦心距为r,边长为a,则R、r、a之间有怎么的数量关系?周长、面积?
三正多边形的中心、半径、中心角、弦心距、边长之间的关系如图:请指出圆内接正六边形的中心、半径、中心角、弦心距.若设半径为R、弦心距为r,边长为a,则R、r、a之间有怎么的数量关系?周长、面积?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com