
【题目】如图,已知函数y=x+1和y=ax+3的图象交于点P,点P的横坐标为1,
(1)关于x,y的方程组![]() 的解是 ;
的解是 ;
(2)a= ;
(3)求出函数y=x+1和y=ax+3的图象与x轴围成的几何图形的面积.

【答案】(1)![]() ;(2)-1;(3)4
;(2)-1;(3)4
【解析】
(1)先求出点P为(1,2),再把P点代入解析式即可解答.
(2)把P(1,2)代入y=ax+3,即可解答.
(3)根据y=x+1与x轴的交点为(﹣1,0),y=﹣x+3与x轴的交点为(3,0),即可得到这两个交点之间的距离,再根据三角形的面积公式,即可解答.
(1)把x=1代入y=x+1,得出y=2,
函数y=x+1和y=ax+3的图象交于点P(1,2),
即x=1,y=2同时满足两个一次函数的解析式.
所以关于x,y的方程组![]() 的解是
的解是![]() .
.
故答案为![]() ;
;
(2)把P(1,2)代入y=ax+3,
得2=a+3,解得a=﹣1.
故答案为﹣1;
(3)∵函数y=x+1与x轴的交点为(﹣1,0),
y=﹣x+3与x轴的交点为(3,0),
∴这两个交点之间的距离为3﹣(﹣1)=4,
∵P(1,2),
∴函数y=x+1和y=ax+3的图象与x轴围成的几何图形的面积为:![]() ×4×2=4.
×4×2=4.


科目:初中数学 来源: 题型:
【题目】目前节能灯在城市已基本普及,今年山东省面向县级及农村地区推广节能灯,为响应号召,某商场计划购进甲、乙两种节能灯共1200只,这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲 | 25 | 30 |
乙 | 45 | 60 |
(1)如何进货,进货款恰好为46000元?
(2)如何进货,商场销售完节能灯时获利最多且不超过进货价的30%,此时利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《代数学》中记载,形如x2+10x=39的方程,求正数解的几何方法是:“如图1,先构造一个面积为x2的正方形,再以正方形的边长为一边向外构造四个面积为![]() x的矩形,得到大正方形的面积为39+25=64,则该方程的正数解为8-5=3”,小聪按此方法解关于x的方程x2+6x+m=0时,构造出如图2所示的图形,己知阴影部分的面积为36,则该方程的正数解为( )
x的矩形,得到大正方形的面积为39+25=64,则该方程的正数解为8-5=3”,小聪按此方法解关于x的方程x2+6x+m=0时,构造出如图2所示的图形,己知阴影部分的面积为36,则该方程的正数解为( )

A.6B.3![]() -3C.3
-3C.3![]() -2D.3
-2D.3![]() -
-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人进行比赛的路程与时间的关系如图所示.
(1)这是一场________米比赛;
(2)前一半赛程内________的速度较快,最终________赢得了比赛;
(3)两人第________秒在途中相遇,相遇时距终点________米;
(4)甲在前8秒的平均速度是多少?甲在整个赛程的平均速度是多少?乙在前8秒的平均速度是多少?乙在整个赛程的平均速度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线![]() 相交于点A(m,3),B(-6,n),与x轴交于点C.
相交于点A(m,3),B(-6,n),与x轴交于点C.
(1)求直线y=kx+b(k≠0)的解析式;
(2)若点P在x轴上,且S△ACP=![]() S△BOC,求点P的坐标(直接写出结果).
S△BOC,求点P的坐标(直接写出结果).

查看答案和解析>>
科目:初中数学 来源: 题型:
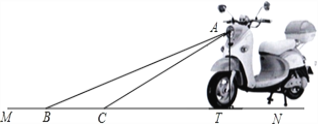
【题目】为响应国家的“节能减排”政策,某厂家开发了一种新型的电动车,如图,它的大灯A射出的光线AB、AC与地面MN的夹角分别为22°和31°,AT⊥MN,垂足为T,大灯照亮地面的宽度BC的长为![]() m.
m.
(1)求BT的长(不考虑其他因素).
(2)一般正常人从发现危险到做出刹车动作的反应时间是0.2s,从发现危险到电动车完全停下所行驶的距离叫做最小安全距离.某人以20km/h的速度驾驶该车,从做出刹车动作到电动车停止的刹车距离是![]() ,请判断该车大灯的设计是否能满足最小安全距离的要求(大灯与前轮前端间水平距离忽略不计),并说明理由.
,请判断该车大灯的设计是否能满足最小安全距离的要求(大灯与前轮前端间水平距离忽略不计),并说明理由.
(参考数据:sin22°≈![]() ,tan22°≈
,tan22°≈![]() ,sin31°≈
,sin31°≈![]() ,tan31°≈
,tan31°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2,已知点A,B是数轴上的点,请参照图并思考,完成下列各题.
(1)如果点A表示数-3,将点A向右移动7个单位长度,那么终点B表示的数是_____,A,B两点间的距离是_____;
(2)如果点A表示数3,将A点向左移动7个单位长度,再向右移动5个单位长度,那么终点表示的数是_____,A,B两点间的距离为_____;
(3)如果点A表示数-4,将A点向右移动168个单位长度,再向左移动256个单位长度,那么终点B表示的数是_____,A、B两点间的距离是_____;
(4)一般地,如果A点表示的数为m,将A点向右移动n个单位长度,再向左移动p个单位长度,那么请你猜想终点B表示什么数?A,B两点间的距离为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对某一个函数给出如下定义:若存在实数M>0,对于任意的函数值y,都满足﹣M≤y≤M,则称这个函数是有界函数,在所有满足条件的M中,其最小值称为这个函数的边界值.例如,如图中的函数是有界函数,其边界值是1.
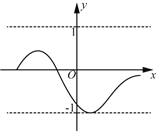
(1)分别判断函数 y=![]() (x>0)和y=x+1(﹣4≤x≤2)是不是有界函数?若是有界函数,求其边界值;
(x>0)和y=x+1(﹣4≤x≤2)是不是有界函数?若是有界函数,求其边界值;
(2)若函数y=﹣x+1(a≤x≤b,b>a)的边界值是2,且这个函数的最大值也是2,求b的取值范围;
(3)将函数 y=x2(﹣1≤x≤m,m≥0)的图象向下平移m个单位,得到的函数的边界值是t,当m在什么范围时,满足![]() ≤t≤1?
≤t≤1?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1)在RtΔABC中,∠ACB=900,∠B=600,在图中作出∠ACB的三等分线CD,CE.(要求:尺规作图,保留痕迹,不定作法)
(2)由(1)知,我们可以用尺规作出直角的三等分线,但是仅仅使用尺规却不能把任意一个角分成三等分,为此,人们发明了许多等分角的机械器具,如图(2)是用三张硬纸片自制的一个最简单的三分角器,与半圆O相接的AB带的长度与半圆的半径相等:BD带的长度任意,它的一边与直线AC形成一个直角,且志半圆相切于点B,假设需要将∠KSM三等分,如图(3),首先将角的顶点S置于BD上,角的一边SK经过点A,另一边SM与半圆相切,连接SO,则SB,SO为∠KSM的三等分线,请你证明。

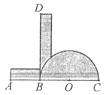

图(1) 图(2) 图(3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com