
⊙O的半径为5,AB是⊙O的直径,点C在⊙O上,点D在直线AB上.
(1)如图(1),已知∠BCD=∠BAC,求证:CD是⊙O的切线;
(2)如图(2),CD与⊙O交于另一点E,BD:DE:EC=2;3:5求圆心O到直线CD的距离;
(3)若图(2)中的点D是直线AB上的动点,点D在运动过程中,会出现在C,D,E三点中,其中一点是另两点连线的中点的情况,问这样的情况出现几次?

(1)证明见解析;(2)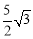 ;(3)三次.
;(3)三次.
【解析】
试题分析:(1)连接OC,证明OC⊥CD即可.
(2)连接OC、OE,过点O作OF⊥CE于点F,证明△BCD∽△EAD,得比例式 ,即
,即 ,根据BD:DE:EC=2:3:5,可设BD=2k,DE=3k,EC=5k,代入求出k即可得BD=2,DE=3,EC=5,从而根据勾股定理即可求得OF.
,根据BD:DE:EC=2:3:5,可设BD=2k,DE=3k,EC=5k,代入求出k即可得BD=2,DE=3,EC=5,从而根据勾股定理即可求得OF.
(3)分点D在⊙O外,点E是CD中点和点D在⊙O内,点D是CE中点两种情况讨论即可.
试题解析:【解析】
(1)证明:如答图1,连接OC,
∵OA=OC,∴∠OAC=∠OCA.
又∵AB是⊙O的直径,∴∠ACB=90°.
又∵∠BCD=∠BAC,∴∠BCD =∠OCA.
∴∠OCD=∠BCD +∠OCB=90°,即OC⊥CD.
∴CD是⊙O的切线.

(2)如答图2,∵∠ADE=∠CDB,∠BCD=∠EAD,∴△BCD∽△EAD.
∴ ,即
,即 .
.
又∵BD:DE:EC=2:3:5,∴可设BD=2k,DE=3k,EC=5k.
又∵⊙O的半径为5,∴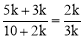 ,解得k=1.
,解得k=1.
∴BD=2,DE=3,EC=5.
连接OC、OE,过点O作OF⊥CE于点F,
则△OEC是等边三角形, EF= CE=
CE= .
.
∴根据勾股定理得
OF= .
.
∴圆心O到直线CD的距离是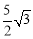 .
.

(3)这样的情形共有出现三次:当点D在⊙O外时,点E是CD中点,有如答图3,4的两种情形;当点D在⊙O内时,点D是CE中点,有如答图5的一种情形.

考点:1.圆的综合题;2.单动点问题;3.等腰三角形的性质;4.圆周角定理;5.切线的判定;6.相似三角形的判定和性质;7.等定系数法的应用;8. 等边三角形的判定和性质;9.勾股定理;10.分类思想和数形结合思想的应用.


科目:初中数学 来源:2014年初中毕业升学考试(江苏南京卷)数学(解析版) 题型:填空题
已知二次函数 中,函数y与x的部分对应值如下:
中,函数y与x的部分对应值如下:
| ... | -1 | 0 | 1 | 2 | 3 | ... |
| ...[ | 10 | 5 | 2 | 1 | 2[ | ... |
则当 时,x的取值范围是 .
时,x的取值范围是 .
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西百色卷)数学(解析版) 题型:选择题
在下列叙述中:
①一组对边相等的四边形是平行四边形;
②函数y= 中,y随x的增大而减小;
中,y随x的增大而减小;
③有一组邻边相等的平行四边形是菱形;
④有不可能事件A发生的概率为0.0001.
正确的叙述有( )
A.0个 B.1个 C.2个 D.3个
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西百色卷)数学(解析版) 题型:选择题
在3月份,某县某一周七天的最高气温(单位:℃)分别为:12,9,10,6,11,12,17,则这组数据的极差是( )
A.6 B.11 C.12 D.17
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西桂林卷)数学(解析版) 题型:解答题
初中学生带手机上学,给学生带来了方便,同时也带来了一些负面影响。针对这种现象,某校九年级数学兴趣小组的同学调查了若干名家长对“初中学生带手机上学”现象的看法,统计整理并制作了如下的统计图:
(1)这次调查的家长总人数为 人,表示“无所谓”的家长人数为 人;
(2)随机抽查一个接受调查的家长,恰好抽到“很赞同”的家长的概率是 ;
(3)求扇形统计图中表示“不赞同”的扇形的圆心角度数.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西崇左卷)数学(解析版) 题型:选择题
若点A(2,4)在函数y=kx的图象上,则下列各点在此函数图象上的是( )
A.(1,2) B.(﹣2,﹣1) C.(﹣1,2) D.(2,﹣4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com