
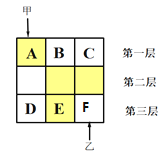
����Ŀ����ͼ��3��3�ķ����Ϊ��������������һ����һö��ɫ����������ڷ���A��B��C���ƶ����ڶ�������ö�̶������ĺ�ɫ��������������һö��ɫ�����������ڷ���D��E��F���ƶ����ס������뷽�������ö��ɫ���鹹�ɸ���ƴͼ��
��1�����ҹ̶���E�����ƶ����ɫ���鹹�ɵ�ƴͼ����Գ�ͼ�εĸ����Ƕ�����
��2�����ס��Ҿ����ڱ����ƶ����û���״ͼ�����б��������ɫ����������ƴͼ����Գ�ͼ�εĸ�����
���𰸡���1��![]() ����2��
����2��![]() .
.
��������
��1�����ҹ̶���E��������ƶ����ɫ���鹹�ɵ�ƴͼһ���ж����ֿ�������������Գ�ͼ�ε��м��ֿ������ɴ˼��ɽ��������
��2��������״ͼ���ɽ��������
��1�����ҹ̶���![]() �����ƶ����ɫ���鹹�ɵ�ƴͼһ����
�����ƶ����ɫ���鹹�ɵ�ƴͼһ����![]() �ֿ�����������
�ֿ�����������![]() ����������Գ�ͼ�����������ҹ̶���
����������Գ�ͼ�����������ҹ̶���![]() �����ƶ����ɫ���鹹�ɵ�ƴͼ����Գ�ͼ�εĸ���Ϊ
�����ƶ����ɫ���鹹�ɵ�ƴͼ����Գ�ͼ�εĸ���Ϊ![]() ��
��
��2���ܹ���![]() �ֵȿ��ܵĽ������ɫ����������ƴͼ����Գ�ͼ�εĽ����
�ֵȿ��ܵĽ������ɫ����������ƴͼ����Գ�ͼ�εĽ����![]() ��������������ĸ���Ϊ
��������������ĸ���Ϊ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
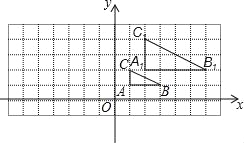
����Ŀ����ͼ����ƽ��ֱ������ϵ�����У�����ABC����λ�Ʊ任�õ���A1B1C1��
��1����A1B1C1����ABC��λ�Ʊ��� ��
��2��������A1B1C1����y��ԳƵ���A2B2C2��
��3�����P��a��b��Ϊ��ABC��һ�㣬�����������α任��P����A2B2C2�ڵĶ�Ӧ��P2�������� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڶ۽����������������Ǻ���ֵ���£�sin����sin (180������)��cos������cos (180������)����һ�������ε������ڽǵı���1��1��4��A��B����������ε��������㣬sinA��cosB�Ƿ���4x2��mx��1��0����������ȵ�ʵ��������m��ֵ����A�͡�B�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
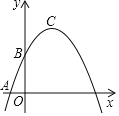
����Ŀ����ƽ��ֱ������ϵxOy�У���ͼ������֪������y=��![]() x2+bx+c������A����1��0���͵�B��0��
x2+bx+c������A����1��0���͵�B��0��![]() ��������ΪC����D����Գ�������λ�ڵ�C�·������߶�DC�Ƶ�D��˳ʱ�뷽����ת90������C�����������ϵĵ�P����
��������ΪC����D����Գ�������λ�ڵ�C�·������߶�DC�Ƶ�D��˳ʱ�뷽����ת90������C�����������ϵĵ�P����
��1�������������ߵı���ʽ��
��2�����߶�CD�ij���
��3����������ƽ�ƣ�ʹ�䶥��C�Ƶ�ԭ��O��λ�ã���ʱ��P���ڵ�E��λ�ã������M��y���ϣ�����O��D��E��MΪ������ı������Ϊ8�����M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
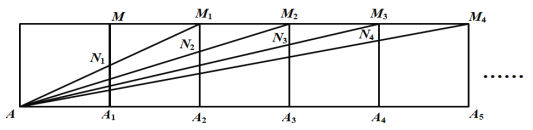
����Ŀ����2019���߳�Ϊ1�������ΰ���ͼ��ʾ�ķ�ʽ����,��A��A1��A2��A3������A2019�͵�M��M1��M2������M2018�������εĶ���,����A1M��A2M1��A3M2������A2018�ֱ������εı�A1M��A2M1��A3M2������A2018M2017�ڵ�N1��N2��N3����N2018,�ı���M1N1A1A2�������![]() ,�ı���M2N2A2A3�������
,�ı���M2N2A2A3�������![]() ,��,��
,��,��![]() �� ��
�� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������y��![]() (k��0��k�dz���)��ͼ�����P(��3,5)��
(k��0��k�dz���)��ͼ�����P(��3,5)��
(1)��˷����������Ľ���ʽ��
(2)�ں���ͼ����������(a1��b1)��(a2��b2)����a1��a2�����ж�b1��b2�Ĵ�С��ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����12�֣���ͼ��ʾ�������Ľ����������ߺͳ����ι��ɣ������εij���12 m������4 m������ͼ����ʾ��ֱ������ϵ�������߿�����y=![]() x2+bx+c��ʾ�����������ϵĵ�C��OB��ˮƽ����Ϊ3 m��������OA�ľ���Ϊ
x2+bx+c��ʾ�����������ϵĵ�C��OB��ˮƽ����Ϊ3 m��������OA�ľ���Ϊ![]() m.
m.
��1���������ߵĺ�����ϵʽ�������������D������OA�ľ��룻
��2��һ������������һ�����弯װ����Ϊ6m����Ϊ4m�������������˫������ô���������ܷ�ȫͨ����
��3������������������Ҫ��װ���ŵƣ�ʹ���������ĸ߶���ȣ�����������ĸ߶Ȳ�����8m����ô���ŵƵ�ˮƽ������С�Ƕ����ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x�ķ��̣�k��1��x2+2kx+2=0��
��1����֤������kΪ��ֵ����������ʵ������
��2����x1��x2�Ƿ��̣�k��1��x2+2kx+2=0������������![]() ��S��ֵ��Ϊ2�����ܣ������ʱk��ֵ�������ܣ���˵�����ɣ�
��S��ֵ��Ϊ2�����ܣ������ʱk��ֵ�������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ��ֱ�ڵ���ĵ���AB��һ�ֽ�CD�̶���CD������45��нǣ���CDB=45�㣩����C���Ϸ�2�״��ӹ���һ������ED��ED������53��нǣ���EDB=53�㣩����ô����ED�ij���ԼΪ�����ף��������ȷ��1�ף��ο����ݣ�sin53���0.80��cos53���0.60��tan53���1.33��
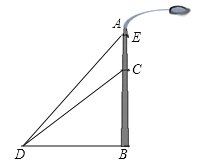
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com