Question

4．从等腰三角形的某一个顶点出发作一条直线，如果恰好能把这个三角形分成两个较小的等腰三角形，则原等腰三角形的顶角是36°，90°，108°，$\frac{180°}{7}$  度．

Answer 1

分析 首先根据题意画出符合题意的所有图形，然后利用等腰三角形求解即可求得答案．

解答 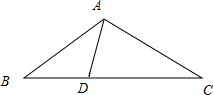解：（1）如图，△ABC中，AB=AC，BD=AD，AC=CD，求∠BAC的度数．
∵AB=AC，BD=AD，AC=CD，
∴∠B=∠C=∠BAD，∠CDA=∠CAD，
∵∠CDA=2∠B，
∴∠CAB=3∠B，
∵∠BAC+∠B+∠C=180°，
∴5∠B=180°，
∴∠B=36°，
∴∠BAC=108°．

（2）如图，△ABC中，AB=AC，AD=BD=CD，求∠BAC的度数．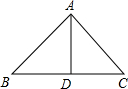
∵AB=AC，AD=BD=CD，
∴∠B=∠C=∠DAC=∠DAB
∴∠BAC=2∠B
∵∠BAC+∠B+∠C=180°，
∴4∠B=180°，
∴∠B=45°，
∴∠BAC=90°．

（3）如图，△ABC中，AB=AC，BD=AD=BC，求∠BAC的度数．
∵AB=AC，BD=AD=BC，
∴∠B=∠C，∠A=∠ABD，∠BDC=∠C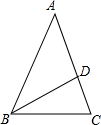
∵∠BDC=2∠A，
∴∠C=2∠A=∠B，
∵∠A+∠ABC+∠C=180°，
∴5∠A=180°，
∴∠A=36°．

（4）如图，△ABC中，AB=AC，BD=AD，CD=BC，求∠BAC的度数．
假设∠A=x°，AD=BD，
∴∠DBA=x°，
∵AB=AC，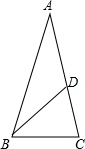
∴∠C=$\frac{180-x}{2}$，
∵CD=BC，
∴∠BDC=2x=∠DBC=$\frac{180-x}{2}$-x，
解得：x=$\frac{180}{7}$．
∴∠A=$\frac{180°}{7}$．
故答案为：36°，90°，108°，$\frac{180°}{7}$．

点评 此题主要考查等腰三角形的性质，三角形外角的性质及三角形内角和定理的综合运用．注意分类讨论思想的应用是解此题的关键．