
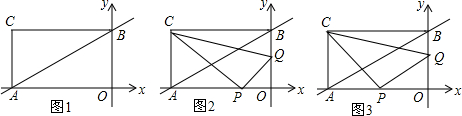
���� ��1�����ݾ��ε������ʽ���ɵ�B�����꣬���ݴ���ϵ�������ɵú�������ʽ��
��2������ͼ�θ�����ɵù���t�ķ��̣����ݽⷽ�̣��ɵô𰸣�
��3�����ݹ��ɶ��������ɶ����涨�����ɵá�NPQ=90�㣬��PON=45�㣬���ݴ���ϵ�������ɵú�������ʽ�������Ա����뺯��ֵ�Ķ�Ӧ��ϵ���ɵô𰸣�
��� �⣺��1����ֱ��y=kx+4k��x�ύ�ڵ�A����y�ύ�ڵ�B����
��x=0ʱ��y=4k����B������Ϊ��0��4k����
��y=0ʱ��kx+4k=0�����x=-4������-4��0����
��AO��BOΪ�ڱ�������AOBC���������8����
4��4k=8�����k=$\frac{1}{2}$��
ֱ��AB�Ľ���ʽ��y=$\frac{1}{2}$x+2��
��2���ɵ�P�ӵ�O���������߶�OA���յ�A�˶����ٶ�Ϊÿ��2����λ���ȣ���Q�ӵ�B���������߶�BO���յ�O�˶����ٶ�Ϊÿ��1����λ���ȣ���
PO=2t��AP=4-2t��QB=t��OQ=2-t��
��S��CPQ=S����ACBO-S��ACP-S��POQ-S��BCQ=$\frac{13}{4}$��
8-$\frac{1}{2}$��4-2t����2-$\frac{1}{2}$•2t��2-t��-$\frac{1}{2}$��4t=$\frac{13}{4}$��
���t=$\frac{1}{2}$��t=$\frac{3}{2}$��
��t=$\frac{1}{2}$��t=$\frac{3}{2}$ʱ����CPQ�����Ϊ$\frac{13}{4}$��
��3�����ڣ���M����Ϊ��-$\frac{1}{3}$��0��
��ͼ��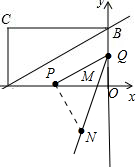
t=1ʱ��P��-2��0����Q��0��1����
ȡN��-1��-2����
PQ2=5��PN25��BN2=10��
PQ2+PN2=NQ2��PQ=PN��
��NPQ=90�㣬��PON=45�㣮
��NQ�Ľ���ʽΪy=kx+b����Q��N��������룬��
$\left\{\begin{array}{l}{b=1}\\{-k+b=-2}\end{array}\right.$��
���$\left\{\begin{array}{l}{b=1}\\{k=3}\end{array}\right.$��
NQ�Ľ���ʽΪy=3x+1��
��y=0ʱ��3x+1=0��
���x=-$\frac{1}{3}$��
��M��-$\frac{1}{3}$��0��
���� ���⿼����һ�κ����ۺ��⣬���þ��е�����ó�B�������ǽ���ؼ�������ͼ�θ���ó�����t�ķ����ǽ���ؼ������ù��ɶ��������ɶ������涨���ó���PQN�ǽ���ؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ʵ��a��b��c����������ͼ��ʾ������|a+b|+a-$\sqrt{c^2}$-|b-c|��
ʵ��a��b��c����������ͼ��ʾ������|a+b|+a-$\sqrt{c^2}$-|b-c|���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���� | �� | ���� | ���� | ���� | ŦԼ |
| ���ʱ�ʱ�� | 0 | +8 | +9 | -4 | -5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ�������������ǣ�������ȷ���ǣ�������
��ͼ�������������ǣ�������ȷ���ǣ�������| A�� | ��A+��B+��C+��D+��E=90�� | B�� | ��A+��B+��C+��D+��E=180�� | ||
| C�� | ��A+��B+��C+��D+��E=270�� | D�� | ��A+��B+��C+��D+��E=360�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com