
 填空完成推理过程:
填空完成推理过程:科目:初中数学 来源: 题型:
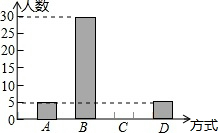 八(3)班在一次班会课上,就“遇见路人摔倒后如何处理”的主题进行讨论,并对全班50名学生的处理方式进行统计,得出相关统计表和统计图(如图)
八(3)班在一次班会课上,就“遇见路人摔倒后如何处理”的主题进行讨论,并对全班50名学生的处理方式进行统计,得出相关统计表和统计图(如图)| 组别 | A | B | C | D |
| 处理方式 | 迅速离开 | 马上救助 | 视情况而定 | 只看热闹 |
| 人数 | m | 30 | n | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△ABC中,A,B,C的坐标分别不(-2,1)(-1,-3),(-5,-1),把△ABC平移使点C移到原点O处,得到△A1B1O.
如图,△ABC中,A,B,C的坐标分别不(-2,1)(-1,-3),(-5,-1),把△ABC平移使点C移到原点O处,得到△A1B1O.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com