
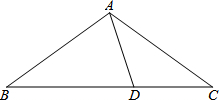
 如图,在△ABC中,AB=AC,D为BC上一点,且AB=BD,AD=DC,求∠C的度数.
如图,在△ABC中,AB=AC,D为BC上一点,且AB=BD,AD=DC,求∠C的度数.  课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案科目:初中数学 来源: 题型:解答题
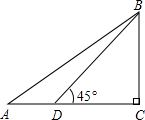 如图,在△ABC,∠C=90°,sin A=$\frac{2}{5}$,D为AC上一点,∠BDC=45°,BD=6$\sqrt{2}$,求AB的长.
如图,在△ABC,∠C=90°,sin A=$\frac{2}{5}$,D为AC上一点,∠BDC=45°,BD=6$\sqrt{2}$,求AB的长.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2a与-3b是同类项 | B. | 0.5x3y2和7x2y3是同类项 | ||
| C. | -a3b2和$\frac{4}{3}$b2a3是同类项 | D. | $\frac{2}{3}$xyz与$\frac{2}{3}$xy是同类项 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 多项式5x2+4x-2的项是5x2,4x,-2 | B. | 多项式x2-2x+3是二次三项式 | ||
| C. | 2×3,$\frac{a+b}{3}$,$\frac{ab}{2}$,$\frac{3a}{π}$都是单项式 | D. | 3-4a中,一次项的系数是-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠ACB=90°,AC=1,将△ABC绕点C顺时针旋转60°至△A′B′C,点A的对应点A′恰好落在AB上,求BB′的长.
如图,在△ABC中,∠ACB=90°,AC=1,将△ABC绕点C顺时针旋转60°至△A′B′C,点A的对应点A′恰好落在AB上,求BB′的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
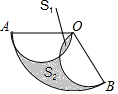 如图,扇形OAB中,OA=OB=2,∠AOB=120°,分别以OA,OB为直径画半圆,若图中两个阴影部分面积分别记为S1与S2,则S2-S1的值是$\frac{1}{3}$π.
如图,扇形OAB中,OA=OB=2,∠AOB=120°,分别以OA,OB为直径画半圆,若图中两个阴影部分面积分别记为S1与S2,则S2-S1的值是$\frac{1}{3}$π.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com