练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．如图，AB∥CD，AD=CD，∠1=70°，则∠2的度数是40°．

    分析 先根据平行线的性质求出∠ACD的度数，再由AC=CD得出∠CAD的度数，根据三角形内角和定理即可得出结论．

    解答 解：∵AB∥CD，∠1=70°，
    ∴∠ACD=∠1=70°．
    ∵AD=CD，
    ∴∠CAD=∠ACD=70°，
    ∴∠2=180°-∠ACD-∠CAD=180°-70°-70°=40°．
    故答案为：40°．

    点评 本题考查的是平行线的性质，用到的知识点为：两直线平行，同位角相等．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    20．解方程：
    （1）9x2-16=0               
    （2）（x+1）3+27=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．（1）因式分解：a（n-1）2-2a（n-1）+a．
    （2）解方程：$\frac{x}{x+1}-1=\frac{2x}{3x+3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．一只螳螂在一圆柱形松树树干的A点处，发现它的正上方B点处有一只小虫子，螳螂想捕到这只虫子，但又怕被发现，于是按如图所示的路线，绕到虫子后面吃掉它．已知树干的周长为20cm，A、B两点的距离为15cm．若螳螂想吃掉在B点的小虫子，求螳螂绕行的最短路程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．一次函数y=mx+n的图象经过一、三、四象限，则化简$\sqrt{（m-n）^{2}}$+$\sqrt{{n}^{2}}$所得的结果m-2n．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．（1）连续投掷一枚均匀的骰子三次，将掷得的点数一次作为百位、十位、个位数字组成一个三位数，求得到个位数字为5的三位数的概率．
    （2）如果将抛掷骰子换成摸球，即在不透明的袋中放入标有数字1，2，3，4，5，6的六个形状，大小完全相同的小球，依次从袋中摸出3个球（每次摸出一个球．且摸出的球不再放回袋中），将球上所标的数字分别作为百位、十位和个位数字组成-个三位数，那么得到个位数字为5的三位数的概率与（1）的结果相同吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

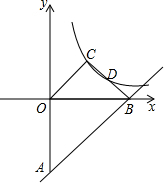    2．如图，直线y=x-4与y轴、x轴分别交于点A、B，点C为双曲线y=$\frac{k}{x}$上一点，OC∥AB，连接BC交双曲线于点D，点D恰好是BC的中点，则k的值是（　　）
    A．$\frac{16}{9}$B．2C．4D．$\frac{4}{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．利用二次函数图象求方程-$\frac{1}{2}$x2+x+2=0的近似解．（精确到0.1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．如图，甲、乙两组同学去野外采集标本，他们从同一地点同时出发，各自沿固定的方向行走．当甲组行走600m、乙组行走630m时，两组的所在地相距870m，那么甲、乙两组同学行走的方向成多少度的角（即图中的α为多少度）？

    查看答案和解析>>

    同步练习册答案