练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．下列图形中，既是轴对称图形又是中心对称图形的是（　　）
    A．
        平行四边形    		B．
         圆    		C．
       正五边形    		D．
       等腰三角形

    分析 根据轴对称图形与中心对称图形的概念求解．

    解答 解：A、平行四边形不是轴对称图形，是中心对称图形．故错误；
    B、圆既是轴对称图形，也是中心对称图形．故正确；
    C、正五边形是轴对称图形，不是中心对称图形．故错误；
    D、等腰三角形不是轴对称图形，不是中心对称图形．故错误．
    故选B．

    点评 本题考查了中心对称图形与轴对称图形的概念：轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合；中心对称图形是要寻找对称中心，旋转180度后与原图重合．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

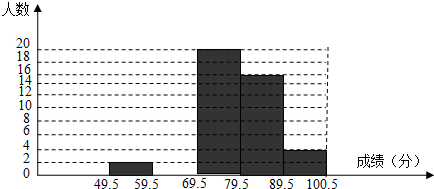
    17．某校七年级的赵明同学对本年级上学期期末考试数学成绩（成绩取整数，满分为100分）随机抽取部分学生的成绩做了统计分析，绘制成不完整的统计表和频数直方图：
     
    分组49.5～59.559.5～69.569.5～79.579.5～89.589.5～100.5合计
    频数2a20164n
    占调查总人数的百分比4%16%m32%b1
    请根据图表提供的信息，解答下列问题：
    （1）分布表中a=8，b0.08；m=0.4，n=50（直接填结果）；
    （2）补全频数分布直方图；
    （3）若成绩为80分及以上者为优秀，已知该年级共有学生600人，请你估计一下这次考试优秀人数约为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．先化简，再求值：（2a+1）（2a-3）-（2a+1）（2a-1），其中a=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．（$\sqrt{3}$+$\sqrt{5}$）（$\sqrt{3}$-$\sqrt{5}$）的值等于（　　）
    A．2B．-2C．$\sqrt{3}$D．$\sqrt{5}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．网瘾低龄化问题已引起社会各界的高度关注，有关部门在全国范围内对年龄在12〜35岁的网瘾人群的年龄进行了随机抽样调查，得到了两个统计图，如图所示，由于胡艳记录不完整，统计12〜17这一段的人数不能确定：但准确地知道AOC是扇形统计图中圆的直径．

    请根据图中的信息，解决下列问题：
    （1）求条形统汁图中a的值；
    （2）求扇形统计图中30～35岁部分的圆心角∠AOD的大小；
    （3）据报道，目前我国12〜35岁网瘾人数约为2000万．请估计其中年龄在18〜29岁的人数．

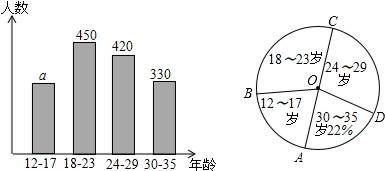
    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如图，O是△ABC内任意一点，试猜想：∠AOB与∠1、∠2、∠C之间的关系，并说明你猜想的正确性．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

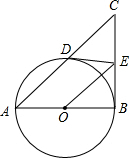    5．如图，在Rt△ABC中，∠ABC=90°，以AB为直径的⊙O与AC边交于点D，过点D作⊙O的切线交BC于点E，连接OE
    （1）证明OE∥AD；
    （2）①当∠BAC=45°时，四边形ODEB是正方形．
         ②当∠BAC=30°时，AD=3DE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

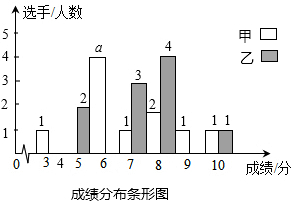    2．某县为选派一个代表队（10名选手）参加市举办的纪念抗战胜利70周年知识竞赛，现有甲、乙两支代表队（各10名选手）参加县里预选，预选时选手得分满分为10分，且选手得分均为整数，成绩达6分及以上为合格，9分或10分为优秀．各队选手成绩分布的条形统计图和成绩统计分析表如下：
    成绩统计分析表
    成绩/队别平均分中位数方差合格率%优秀率%
    甲队6.9m3.419n
    乙队6.8x-13.258x
    （1）请依据图表中的数据，求出条形图中a的值；
    （2）写出表中m、n的值；
    （3）有人说甲队的合格率、优秀率均高于乙队，所以应选派甲队参加市赛，但也有人认为乙队成绩比甲队好．请给出两条支持乙队代表县里参加市赛的理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

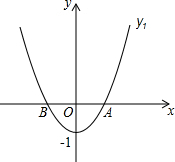    3．如图，在平面直角坐标系中，抛物线y1=x2-1与x轴交于点A和点B（点A在点B的右侧），抛物线y2的解析式为y2=$\frac{1}{1-n}$（x-n）2+n-1（n≠1，直线y3的解析式为y3=x-2．
    （1）试通过计算说明抛物线y2与直线y3均过点A；
    （2）若抛物线y2与x轴的另一交点为C，且有BC=2AB，请求出此时y2的解析式；
    （3）当n≤0时，已知对于x的任意同一个值，所对应三个函数的函数值为y1，y2，y3，请画出它们的大致图象后猜想y1，y2，y3的大小关系并给出证明．

    查看答案和解析>>

    同步练习册答案