
已知:△ABC是边长为4的等边三角形,点O在边AB上,⊙O过点B且分别与边AB,BC相交于点D,E,EF⊥AC,垂足为F.
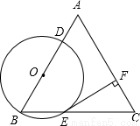
(1)求证:直线EF是⊙O的切线;
(2)当直线DF与⊙O相切时,求:⊙O的半径.
(1)证明见解析;(2)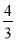 .
.
【解析】
试题分析:(1)连接OE.欲证直线EF是⊙O的切线,只需证明EF⊥AC.利用等边三角形的三个内角都是60°、等腰三角形OBE以及三角形的内角和定理求得同位角∠BOE=∠A=60°,从而判定OE∥AC,所以由已知条件EF⊥AC判定OE⊥EF,即直线EF是⊙O的切线;
(2)连接DF.设⊙O的半径是r.由等边三角形的三个内角都是60°、三条边都相等、以及在直角三角形中30°所对的直角边是斜边的一半求得关于r的方程4-r=2(4r-4),解方程即可.
试题解析:(1)证明:连接OE.
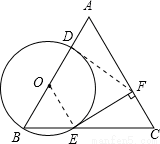
∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°;
在△BOE中,OB=OE,∠B=60°,
∴∠B=∠OEB=∠BOE=60°,
∴∠BOE=∠A=60°,
∴OE∥AC;
∵EF⊥AC,
∴OE⊥EF,即直线EF是⊙O的切线;
(2)【解析】
连接DF.
∵DF与⊙O相切,
∴∠ADF=90°.
设⊙O的半径是r,则EB=r,EC=4-r,AD=4-2r.
在Rt△ADF中,∠A=60°,
∴AF=2AD=8-4r.
∴FC=4r-4;
在Rt△CEF中,∵∠C=60°,∴EC=2FC,
∴4-r=2(4r-4),
解得,r=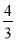 ;
;
∴⊙O的半径是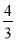 .
.
考点:1.切线的判定与性质;2.等边三角形的判定与性质.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2014-2015学年山东省九年级上学期第三次月考数学试卷(解析版) 题型:填空题
有4条线段,长度分别为2cm,3cm,4cm,6cm,从中任取3条,能构成三角形的概率是 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省滨州地区九年级12月月考数学试卷(解析版) 题型:选择题
若双曲线y= 的图象经过第二、四象限,则k的取值范围是( )
的图象经过第二、四象限,则k的取值范围是( )
A.k>0 B.k<0 C.k≠0 D.不存在
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江西省吉安市朝宗实验学校九年级上学期期中考试数学试卷(解析版) 题型:填空题
一个函数满足如下性质:①它的图象经过点(-1,-2):②它的图象会经过第三象限;③在第三象限,y随x的增大而减小,则这个函数的解析式可以是___________.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江西省吉安市朝宗实验学校九年级上学期期中考试数学试卷(解析版) 题型:选择题
一个用于防震的“L”型包装塑料泡沫如图所示,则该物体的俯视图是( )

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏盐城东台苏东双语学校九年级上学期第一次检测二数学试卷(解析版) 题型:解答题
(本题满分10分)如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作?ABDE,连接AD,EC.

(1)求证:△ADC≌△ECD;
(2)若BD=CD,求证:四边形ADCE是矩形.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市锡山区九年级上学期期中考试数学试卷(解析版) 题型:填空题
 ,则方程的解为___________,方程
,则方程的解为___________,方程 的解是___________.
的解是___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com