
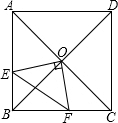
 在正方形ABCD中,O是对角线的交点,过O作OE⊥OF,分别交AB,BC于E,F,若AE=4,CF=3.
在正方形ABCD中,O是对角线的交点,过O作OE⊥OF,分别交AB,BC于E,F,若AE=4,CF=3.分析 (1)由正方形的性质得出OB=OC=OA=OD,∠BAD=∠ABC=∠BCD=90°,∠OBE=∠OCF=45°,证出∠BOE=∠COF,由ASA证明△BOE≌△COF即可;
(2)由全等三角形的性质得出BE=CF=3,同理△AOE≌△BOF,得出BF=AE=4,AB=7,由勾股定理求出EF;由全等三角形的性质得出四边形OEBF的面积=△AOB的面积=$\frac{1}{4}$正方形ABCD的面积,即可得出结果.
解答 (1)证明:∵四边形ABCD是正方形,
∴OB=OC=OA=OD,∠BAD=∠ABC=∠BCD=90°,∠OBE=∠OCF=45°,AC⊥BD,
∴∠BOC=90°,
∵OE⊥OF,
∴∠EOF=90°,
∴∠BOE=∠COF,
在△BOE和△COF中,$\left\{\begin{array}{l}{∠BOE=∠COF}&{\;}\\{OB=OC}&{\;}\\{∠OBE=∠OCF}&{\;}\end{array}\right.$,
∴△BOE≌△COF(ASA);
(2)解:∵△BOE≌△COF,
∴BE=CF=3,
同理:△AOE≌△BOF,
∴BF=AE=4,
∴AB=AE+BE=7,EF=$\sqrt{B{E}^{2}+B{F}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5;
∵△BOE≌△COF,△AOE≌△BOF,
∴四边形OEBF的面积=△BOE的面积+△AOE的面积
=△AOB的面积=$\frac{1}{4}$正方形ABCD的面积
=$\frac{1}{4}$×72=$\frac{49}{4}$.
点评 本题考查了正方形的性质、全等三角形的判定与性质、勾股定理;熟练掌握正方形的性质,并能进行推理计算是解决问题的关键.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:解答题
| 场次 得分 班级 | 1 | 2 | 3 | 4 | 5 |
| 一班 | 85 | 88 | 77 | 75 | 85 |
| 二班 | 95 | 85 | 70 | 80 | 80 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
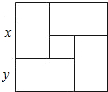 用四个完全一样的长方形和一个小正方形拼成如图所示的大长方形的长和宽,已知大正方形的面积是121,小正方形的面积是9,若用x,y(x>y)表示长方形的长和宽,则下列关系中不正确的是( )
用四个完全一样的长方形和一个小正方形拼成如图所示的大长方形的长和宽,已知大正方形的面积是121,小正方形的面积是9,若用x,y(x>y)表示长方形的长和宽,则下列关系中不正确的是( )| A. | x+y=11 | B. | x2+y2=180 | C. | x-y=3 | D. | x•y=28 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com