
【题目】正方形和下列边长相同的正多边形地砖组合中,不能够铺满地面的是( )
A. 正三角形 B. 正六边形
C. 正八边形 D. 正三角形和正六边形
【答案】B
【解析】
正多边形的组合能否铺满地面,关键是看位于同一顶点处的几个角之和能否为360°.若能,则说明能铺满;反之,则说明不能铺满.
A. 正三角形的每个内角是60°,正方形的每个内角是90°,
∵3×60°+2×90°=360°,∴能铺满地面;
B. 正方形的每个内角是90°,正六边形的每个内角是120°,
∵90°m+120°n=360°, m=4![]() n,显然n取任何整数时,m不能得正整数,故不能铺满;
n,显然n取任何整数时,m不能得正整数,故不能铺满;
C. 正方形的每个内角是90°,正八边形的每个内角是135°,
∵90°+2×135°=360°,∴能铺满地面;
D. 正三角形的每个内角是60°,正方形的每个内角是90°,正六边形的每个内角是120°, ∵60°+2×90°+120°=360°,∴能铺满地面。
故选:B.


 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=2,AC=BC= ![]() .
.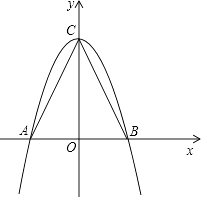
(1)以AB所在的直线为x轴,AB的垂直平分线为y轴,建立直角坐标系如图,请你分别写出A、B、C三点的坐标;
(2)求过A、B、C三点且以C为顶点的抛物线的解析式;
(3)若D为抛物线上的一动点,当D点坐标为何值时,S△ABD= ![]() S△ABC;
S△ABC;
(4)如果将(2)中的抛物线向右平移,且与x轴交于点A′B′,与y轴交于点C′,当平移多少个单位时,点C′同时在以A′B′为直径的圆上(解答过程如果有需要时,请参看阅读材料).
附:阅读材料
一元二次方程常用的解法有配方法、公式法和因式分解法,对于一些特殊方程可以通过换元法转化为一元二次方程求解.如解方程:y4﹣4y2+3=0.
解:令y2=x(x≥0),则原方程变为x2﹣4x+3=0,解得x1=1,x2=3.
当x1=1时,即y2=1,∴y1=1,y2=﹣1.
当x2=3,即y2=3,∴y3= ![]() ,y4=﹣
,y4=﹣ ![]() .
.
所以,原方程的解是y1=1,y2=﹣1,y3= ![]() ,y4=﹣
,y4=﹣ ![]() .
.
再如x2﹣2=4 ![]() ,可设y=
,可设y= ![]() ,用同样的方法也可求解.
,用同样的方法也可求解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线 ![]() 与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,连接BC.
与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,连接BC.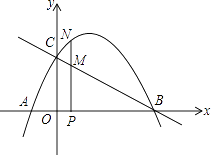
(1)求点A、B、C的坐标.
(2)点P为AB上的动点(点A、O、B除外),过点P作直线PN⊥x轴,交抛物线于点N,交直线BC于点M.设点P到原点的值为t,MN的长度为s,求s与t的函数关系式.
(3)在(2)的条件下,试求出在点P运动的过程中,由点O、P、N围成的三角形与Rt△COB相似时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,直线AB:y=﹣x+b交y轴于点A,交x轴于点B,S△AOB=8.
(1)求点B的坐标和直线AB的函数表达式;
(2)直线a垂直平分OB交AB于点D,交x轴于点E,点P是直线a上一动点,且在点D的上方,设点P的纵坐标为m.
①用含m的代数式表示△ABP的面积;
②当S△ABP=6时,求点P的坐标;
③在②的条件下,在坐标轴上,是否存在一点Q,使得△ABQ与△ABP面积相等?若存在,直接写出点Q的坐标,若不存在,请说明理由.
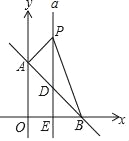
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一台自动测温仪记录的图象,它反映了我市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )

A. 凌晨4时气温最低为-3℃
B. 14时气温最高为8℃
C. 从0时至14时,气温随时间增长而上升
D. 从14时至24时,气温随时间增长而下降
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,MN为⊙O的直径,A、B是⊙O上的两点,过A作AC⊥MN于点C,过B作BD⊥MN于点D,P为DC上的任意一点,若MN=20,AC=8,BD=6,则PA+PB的最小值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小明和爸爸在400米的环形跑道上骑车锻炼,他们在同一地点沿着同一方向同时出发,骑行结束后两人有如下对话:

(1)他们的对话内容,求小明和爸爸的骑行速度,
(2)一次追上小明后,在第二次相遇前,再经过多少分钟,小明和爸爸相距50m?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com