
【题目】阅读下列材料,完成(1)~(3)题:
数学课上,老师出示了这样一道题:
如图1,△ABC中,AB=AC,∠BAC=90°,点D是BC的中点,E是AC的中点,经过点A、C作射线BE的垂线,垂足分别为点F、G,连接AG.探究线段DF和AG的关系.某学习小组的同学经过思考后,交流了自己的想法:
小明:“经过观察和度量,发现∠ABF和∠ACG相等.”小刚:“经过观察和度量,发现有两条线段和AF相等.”
小伟:“通过构造全等三角形,经过进一步推理,可以得到线段DF和AG的关系.”
……
老师:“若点E不是AC的中点,其他条件不变(如图2),可以求出![]() 的值.”
的值.”
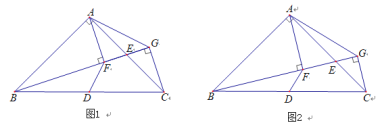
(1)求证:AF=FG;
(2)探究线段DF和AG的关系,并证明;
(3)直接写出![]() 的值.
的值.
【答案】(1)证明见解析;(2)![]() ,证明见解析;(3)
,证明见解析;(3)![]() .
.
【解析】
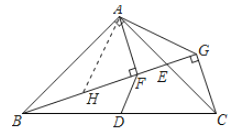
(1)如图1中,作AH⊥AG交BG于H.证明△ABH≌△ACG(ASA)可得结论.
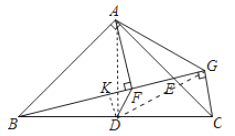
(2)结论:AG=2DF,DF⊥AG.如图2中,连接AD,DG,作DK⊥BG于K.证明△DFA≌△DFG(SSS),推出∠ADF=∠GDF,可得DF⊥AG,再证明DF=![]() DK,AG=
DK,AG=![]() AF,AF=CG=2DK即可解决问题.
AF,AF=CG=2DK即可解决问题.
(3)利用(2)中结论即可解决问题.
(1)证明:过点![]() 作
作![]() ,交
,交![]() 于
于![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
又∵![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
(2)证明:作![]() .如图:
.如图:
∵![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
(3)由(2)可知:CG=2DK,DF=![]() DK,
DK,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() ,
,![]() 两点
两点![]() 在
在![]() 左侧),与
左侧),与![]() 轴交于点
轴交于点![]() ,顶点为
,顶点为![]() .
.
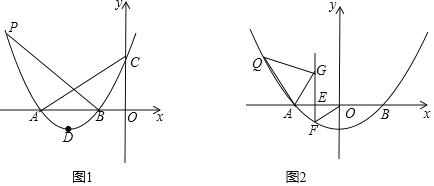
(1)当![]() 时,求四边形
时,求四边形![]() 的面积
的面积![]() ;
;
(2)在(1)的条件下,在第二象限抛物线对称轴左侧上存在一点![]() ,使
,使![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)如图2,将(1)中抛物线沿直线![]() 向斜上方向平移
向斜上方向平移![]() 个单位时,点
个单位时,点![]() 为线段
为线段![]() 上一动点,
上一动点,![]() 轴交新抛物线于点
轴交新抛物线于点![]() ,延长
,延长![]() 至
至![]() ,且
,且![]() ,若
,若![]() 的外角平分线交点
的外角平分线交点![]() 在新抛物线上,求
在新抛物线上,求![]() 点坐标.
点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店在节日期间开展优惠促销活动:购买原价超过500元的商品,超过500元的部分可以享受打折优惠.若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)的函数关系的图像如图所示,则超过500元的部分可以享受的优惠是( )

A. 打六折B. 打七折C. 打八折D. 打九折
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)求出y与x的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系h=20t﹣5t2.下列叙述正确的是( )

A. 小球的飞行高度不能达到15m
B. 小球的飞行高度可以达到25m
C. 小球从飞出到落地要用时4s
D. 小球飞出1s时的飞行高度为10m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解学生平均每天“诵读经典”的时间,在全校范围内随机抽查了部分学生进行调查统计(设每天的诵读时间为![]() 分钟),将调查统计的结果分为四个等级:Ⅰ级
分钟),将调查统计的结果分为四个等级:Ⅰ级![]() 、Ⅱ级
、Ⅱ级![]() 、Ⅲ级
、Ⅲ级![]() 、Ⅳ级
、Ⅳ级![]() .将收集的数据绘制成如下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
.将收集的数据绘制成如下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
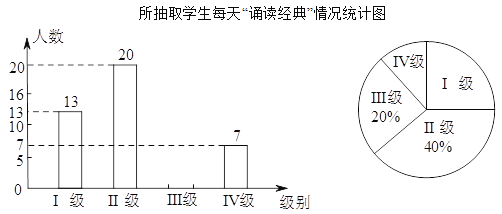
(![]() )请补全上面的条形图.
)请补全上面的条形图.
(![]() )所抽查学生“诵读经典”时间的中位数落在__________级.
)所抽查学生“诵读经典”时间的中位数落在__________级.
(![]() )如果该校共有
)如果该校共有![]() 名学生,请你估计该校平均每天“诵读经典”的时间不低于
名学生,请你估计该校平均每天“诵读经典”的时间不低于![]() 分钟的学生约有多少人?
分钟的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,过
,过![]() ,
,![]() ,
,![]() 三点作圆,点
三点作圆,点![]() 在第一象限部分的圆上运动,连结
在第一象限部分的圆上运动,连结![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 的延长线于点
的延长线于点![]() ,下列说法:①
,下列说法:①![]() ;②
;②![]() ;③
;③![]() 的最大值为10.其中正确的是( )
的最大值为10.其中正确的是( )
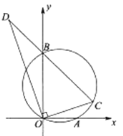
A. ①②B. ②③C. ①③D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小敏为了解本市的空气质量情况,从环境监测网随机抽取了若干天的空气质量情况作为样本进行统计,绘制了如图所示的条形统计图和扇形统计图(部分信息未给出).
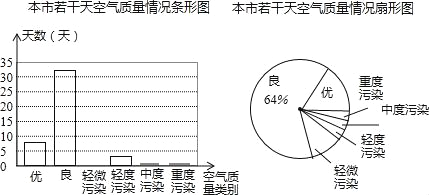
根据以上信息,如下结论错误的是( )
A.被抽取的天数为50天
B.空气轻微污染的所占比例为10%
C.扇形统计图中表示优的扇形的圆心角度数57.6°
D.估计该市这一年达到优和良的总天数不多于290天
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=k1x+2与反比例函数![]() 的图象交于点A(4,m)和B(﹣8,﹣2)与x轴交于点C.过点A作AD⊥x轴于点D
的图象交于点A(4,m)和B(﹣8,﹣2)与x轴交于点C.过点A作AD⊥x轴于点D
(1)求一次函数与反比例函数的解析式.
(2)根据函数图象知,当y1>y2时,x的取值范围是 ;
(3)连接BD,求△ABD的面积
(4)点P是反比例函数在第一象限的图象上一点,设直线OP与线段AD交于点E,当△ODE∽△CDA时,求点P的坐标.
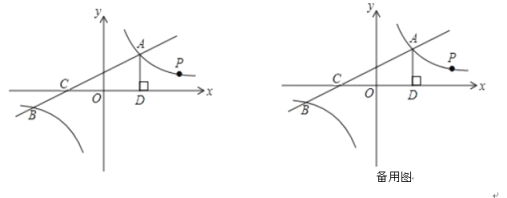
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com