
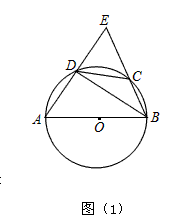
| 解:(1)连结OD,OC, ∵AD⊥BD, ∴弦AB是⊙O的直径, ∴OD=OC= 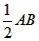 =1=CD, =1=CD,∴△DOC是等边三角形, ∴∠DOC=60°, ∴∠DBC=30°, ∵AD⊥BD, ∴∠EDB=90°, ∴ 在Rt△BD E中,∠E=90°-∠DBC=90°-30°=60°; |
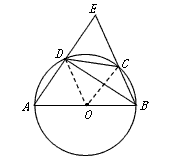 |
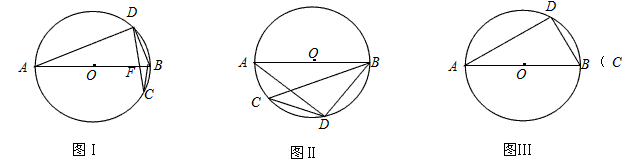
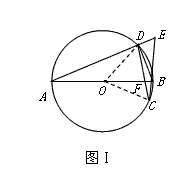
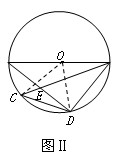
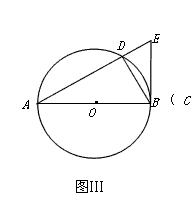
| (2)① 如图Ⅰ,连结OD,OC,由(1)知: ∴∠DOC=60°, ∵∠CDB= 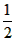 ∠BOC,∠DCB= ∠BOC,∠DCB=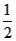 ∠DOB, ∠DOB,而∠DBE=∠CDB+∠DCB, ∴∠DBE= 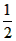 ∠BOC+ ∠BOC+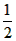 ∠DOB= ∠DOB=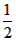 ∠DOC=30°, ∠DOC=30°,∵AD⊥BD, ∴∠EDB=90°, ∴在Rt△BDE中, ∠E=90°-∠DBC=90°-30°=60°, ② 如图Ⅱ,连结OD,OC, 由(1)知:∠DOC=60°, ∴∠DBC=30°, ∵AD⊥BD, ∴∠ADB=90°, ∴ 在Rt△BD E中,∠BED=90°-∠DBC=90°-30°=60°, ③ 如图Ⅲ,当点C与点B重合时,直线BE与⊙O只有一个公共点, ∴ EB为⊙O的切线, ∴∠ABE=90°, ∵AD⊥BD, ∴∠ADB=90°, 又∵点C与点B重合, ∴DB=CD=1, 在Rt△ABD中, ∵ 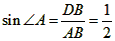 , ,∴∠A=30°, ∴在Rt△BD E中,∠E=90°-∠A=90°-30°=60°, 综上所述:如果C、D点在⊙O上运动,且保持弦CD的长度不变,那么直线AD、BC相交所成锐角的大小不会改变。 |
   |


科目:初中数学 来源: 题型:
 延长线于点D.
延长线于点D.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:在⊙O中,AB是直径,AC是弦,OE⊥AC于点E,过点C作直线FC,使∠FCA=∠AOE,交AB的延长线于点D.
已知:在⊙O中,AB是直径,AC是弦,OE⊥AC于点E,过点C作直线FC,使∠FCA=∠AOE,交AB的延长线于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com