【题目】有五组数：①25，7，24；②16，20，12；③9，40，41；④4，6，8；⑤32，42，52，以各组数为边长，能组成直角三角形的个数为（ ）
A. 1 B. 2 C. 3 D. 4
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案科目：初中数学 来源： 题型：
【题目】对于上抛物体，在不计空气阻力的情况下，有如下关系式：h=v0t﹣
gt2，其中h（米）是上抛物体上升的高度，v0（米/秒）是上抛物体的初速度，g（米/秒2）是重力加速度，t（秒）是物体抛出后所经过的时间，如图是h与t的函数关系图．
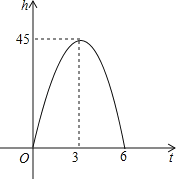
（1）求：v0和g；
（2）几秒后，物体在离抛出点40米高的地方？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】十八世纪瑞士数学家欧拉证明了简单多面体中顶点数（
）、面数（
）、棱数（
）之间存在的一个有趣的关系式，被称为欧拉公式，请你观察下列几种简单多面体模型，解答下列问题：
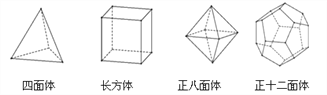
（1）根据上面多面体模型，完成表格中的空格；
多面体 | 顶点数（ | 面数（ | 棱数（ |
四面体 |
|
| |
长方体 |
|
|
|
正八面体 |
|
| |
正十二面体 |
|
|
|
（1）你发现顶点数（）、面数（）、棱数（）之间存在的关系式是_______.
（2）正十二面体有
个顶点，那它有______条棱；
（3）一个多面体的面数比顶点数大
，且有
条棱，则这多面体的顶点数是______；
（4）某个玻璃饰品的外形是简单多面体，它的外表是由三角形和八边形两种多边形拼接而成，且有
个顶点，每个顶点处都有
条棱，设该多面体表面三角形的个数为
个，八边形的个数为
个，求
的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知菱形ABCD，AB=AC，E、F分别是BC、AD的中点，连接AE、CF．
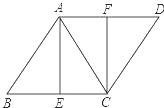
（1）求证：四边形AECF是矩形；
（2）若AB=6，求菱形的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】若关于x的一元二次方程ax2+2x﹣5=0的两根中有且仅有一根在0和1之间（不含0和1），则a的取值范围是（ ）
A．a＜3 B．a＞3 C．a＜﹣3 D．a＞﹣3
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）阅读并填空：如图①，BD、CD分别是△ABC的内角∠ABC、∠ACB的平分线．
试说明∠D=90°+
∠A的理由．
解：因为BD平分∠ABC（已知），
所以∠1= （角平分线定义）．
同理：∠2= ．
因为∠A+∠ABC+∠ACB=180°，∠1+∠2+∠D=180°，（ ），
所以∠D = （等式性质）．
即：∠D=90°+∠A．
（2）探究，请直接写出结果，并任选一种情况说明理由：
（i）如图②，BD、CD分别是△ABC的两个外角∠EBC、∠FCB的平分线．试探究∠D与∠A之间的等量关系．
答：∠D与∠A之间的等量关系是 ．
（ii）如图③，BD、CD分别是△ABC的一个内角∠ABC和一个外角∠ACE的平分线．试探究∠D与∠A之间的等量关系．
答：∠D与∠A之间的等量关系是 ．
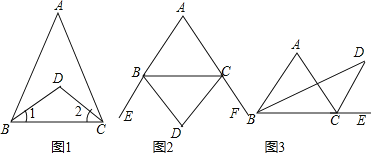
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
