

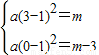

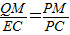
 ,得EC=2(x-1)
,得EC=2(x-1)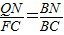
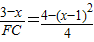 ,得
,得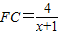
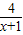 [4+2(x-1)]=
[4+2(x-1)]=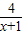 (2x+2)=
(2x+2)=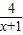 ×2×(x+1)=8
×2×(x+1)=8

科目:初中数学 来源: 题型:
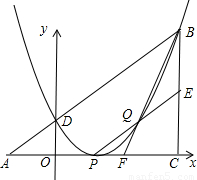
 (2009•株洲)如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.
(2009•株洲)如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.查看答案和解析>>
科目:初中数学 来源:2009年全国中考数学试题汇编《二次函数》(05)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2011年福建省三明市大田二中中考数学模拟试卷(解析版) 题型:解答题
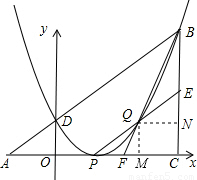
 ,点P在线段AB上运动,点Q、R分别在线段BC、AC上,且使得四边形APQR是矩形.设AP的长为x,矩形APQR的面积为y,已知y是x的函数,其图象是过点(12,36)的抛物线的一部分(如图2所示).
,点P在线段AB上运动,点Q、R分别在线段BC、AC上,且使得四边形APQR是矩形.设AP的长为x,矩形APQR的面积为y,已知y是x的函数,其图象是过点(12,36)的抛物线的一部分(如图2所示).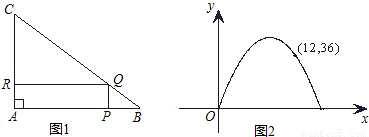
查看答案和解析>>
科目:初中数学 来源:2009年湖南省株洲市中考数学试卷(解析版) 题型:选择题
 (2009•株洲)如图是“北大西洋公约组织”标志的主体部分(平面图),它是由四个完全相同的四边形OABC拼成的.测得AB=BC,OA=OC,OA⊥OC,∠ABC=36°,则∠OAB的度数是( )
(2009•株洲)如图是“北大西洋公约组织”标志的主体部分(平面图),它是由四个完全相同的四边形OABC拼成的.测得AB=BC,OA=OC,OA⊥OC,∠ABC=36°,则∠OAB的度数是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com