
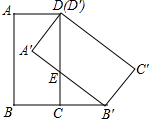
 ČēĶ¼£¬ŌŚ¾ŲŠĪABCDÖŠ£¬BC=1£¬½«¾ŲŠĪABCDČʵćDÄꏱÕėŠż×Ŗ45”ć£¬µĆµ½¾ŲŠĪA”äB”äC”äD”䣬µćB”äĒ”ŗĆĀäŌŚBCµÄŃÓ³¤ĻßÉĻ£¬±ßA”äB”ä½»±ßCDÓŚµćE£®
ČēĶ¼£¬ŌŚ¾ŲŠĪABCDÖŠ£¬BC=1£¬½«¾ŲŠĪABCDČʵćDÄꏱÕėŠż×Ŗ45”ć£¬µĆµ½¾ŲŠĪA”äB”äC”äD”䣬µćB”äĒ”ŗĆĀäŌŚBCµÄŃÓ³¤ĻßÉĻ£¬±ßA”äB”ä½»±ßCDÓŚµćE£®·ÖĪö £Ø1£©ÓɾŲŠĪµÄŠŌÖŹŗĶŠż×ŖµÄŠŌÖŹÅŠ¶Ļ³ö”÷DBB”äŹĒµČŃüČż½ĒŠĪ£»
£Ø2£©·ÖČż¶Ī¼ĘĖć£¬ÓɾŲŠĪµÄŠŌÖŹŠż×ŖµÄŠŌÖŹĻČ¼ĘĖć³öS”÷A”äD”äG£¬SĖıߊĪD”äGEF¼“æÉ£»
£Ø3£©ĻČÓɾŲŠĪµÄŠŌÖŹŗĶŠż×ŖµÄŠŌÖŹ±ķŹ¾³öĻą¹ŲµÄĻ߶Ī£¬ŌŁÓƱȥżŹ½$\frac{AD”ä}{A”äM}=\frac{D”äM}{A”äM}$£¬¼ĘĖć¼“æÉ£®
½ā“š Ö¤Ć÷£ŗ£Ø1£©ČēĶ¼¢Ł£¬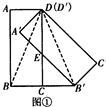
Į¬½ÓDB£¬DB”䣬
”ßĖıߊĪABCDŹĒ¾ŲŠĪ£¬
”ą”ĻBCD=90”ć£¬
”ąDC”ĶBB”䣬
ÓÉŠż×ŖÓŠ£¬DB=DB”䣬
”ąB”äC=BC£»
£Ø2£©ČēĶ¼¢Ś£¬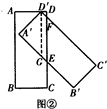
µ±0£¼t”Ü1-$\frac{\sqrt{2}}{2}$Ź±£¬×÷D”äG”ĪDC£¬½»A”äB”äÓŚG£¬
”ßĖıߊĪA”äB”äC”äD”äŹĒ¾ŲŠĪ£¬
”ąA”äB”ä”ĪD”äC”ä
”ąĖıߊĪD”äGEFŹĒĘ½ŠŠĖıߊĪ£¬
ÓÉŠż×ŖÓŠ”ĻA”äD”äG=45”ć£¬
”ßA”äD”ä=1£¬
”ąS”÷A”äD”äG=$\frac{1}{2}$”ĮA”äD”ä2=$\frac{1}{2}$”Į1=$\frac{1}{2}$£¬D”äG=$\sqrt{2}$£¬
ÓÉŌĖ¶ÆŹ±¼äĪŖt£¬
”ąDD”ä=t£¬
”ąSĖıߊĪD”äGEF=D”äG”ĮDD”ä=$\sqrt{2}$t£¬
”ąS=S”÷A”äD”äG+SĖıߊĪD”äGEF=$\frac{1}{2}$+$\sqrt{2}$t£¬
µ±t=1Ź±£¬ČēĶ¼¢Ū£¬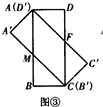
”ßĖıߊĪABCD£¬A”äB”ä”äD”äŹĒ¾ŲŠĪ£¬
”ąĖıߊĪAMCFŹĒĘ½ŠŠĖıߊĪ£¬
”ąS=AM”ĮAD=$\sqrt{2}$A”äD”ä”ĮAD=$\sqrt{2}$”Į1”Į1=$\sqrt{2}$£»
µ±1+$\frac{\sqrt{2}}{2}$”Üt£¼2Ź±£¬ČēĶ¼¢Ü£¬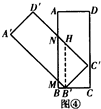
¹żB”ä×÷B”äM”ĪAB£¬
Ķ¬Ąķ£ŗĖıߊĪNMB”äHŹĒĘ½ŠŠĖıߊĪ£¬
”ąMN=B”äH=$\sqrt{2}$B”äC”ä=$\sqrt{2}$
ŌĖ¶ÆŹ±¼äĪŖt£¬
”ąBB”ä=2-t£¬
”ąS=S”÷B”äC”äM+SĖıߊĪNMB”äH
=$\frac{1}{2}$”ĮB”äC”ä2+MN”ĮBB”ä
=$\frac{1}{2}$”Į1+$\sqrt{2}$£Ø2-t£©
=$\frac{1}{2}$+2$\sqrt{2}$-$\sqrt{2}$t£»
£Ø3£©
µćA”ä¹ŲÓŚABµÄ¶Ō³Ęµć¼Ē×÷µćF£¬
”ąA”äF”ĶAB£¬
”ßĖıߊĪABCDĪŖ¾ŲŠĪ£¬
”ąAD”ĶAB£¬
”ąA”äF”ĪAD£¬
”ßÖ±ĻßDFÓė¾ŲŠĪA”äB”äC”äD”äµÄ±ßĘ½ŠŠ
¢ŁČēĶ¼¢Ż£¬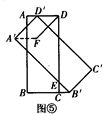
µ±DF”ĪA”äD”䏱£¬ĖıߊĪA”äFDD”äŹĒĘ½ŠŠĖıߊĪ£¬
”ąA”äF=DD”ä=t£¬
”ąAD”ä=1-t£¬
”ßµćA”äÓėF¹ŲÓŚAB¶Ō³Ę£¬
”ąA”äM=FM=$\frac{t}{2}$£¬
”ß”ĻAD”äM=”ĻMA”äF=45”ć£¬
”ąA”äM=$\frac{\sqrt{2}}{2}$t£¬
”ąD”äM=A”äD”ä-A”äM=1-$\frac{\sqrt{2}}{2}$t£¬
”ßAD”ĪA”äF£¬
”ą$\frac{AD”ä}{A”äM}=\frac{D”äM}{A”äM}$£¬
”ą$\frac{1-t}{\frac{t}{2}}=\frac{1-\frac{\sqrt{2}}{2}t}{\frac{\sqrt{2}}{2}t}$£¬
”ąt=2-$\sqrt{2}$£»
¢ŚČēĶ¼¢Ž£¬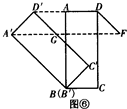
µ±DF”ĪD”äC”䏱£¬ĖıߊĪD”äGFDŹĒĘ½ŠŠĖıߊĪ£¬
”ąGF=DD”ä=t£¬
”ßA”äG=$\sqrt{2}$A”äD”ä=$\sqrt{2}$£¬
”ąA”äF=A”äG+GF=$\sqrt{2}$+t£¬
”ßA”äF=2£Øt-1+$\frac{\sqrt{2}}{2}$£©=2t-2+$\sqrt{2}$£¬
”ą$\sqrt{2}$+t=2t-2+$\sqrt{2}$£¬
”ąt=2£¬
¼“£ŗÖ±ĻßDFÓė¾ŲŠĪA”äB”äC”äD”äµÄ±ßĘ½ŠŠŹ±tµÄÖµĪŖ2-$\sqrt{2}$»ņ2£®
µćĘĄ “ĖĢāŹĒ¼øŗĪ±ä»»×ŪŗĻĢā£¬Ö÷ŅŖæ¼²éĮĖ¾ŲŠĪµÄŠŌÖŹ£¬Šż×ŖµÄŠŌÖŹ£¬Čż½ĒŠĪĆ껿µÄ¼ĘĖć£¬øł¾ŻĢõ¼ž±ķŹ¾³öĻ߶ĪŹĒ½Ó±¾ĢāµÄ¹Ų¼ü£¬ÄѵćŹĒ·Ö¶ĪĒóŗÆŹż½āĪöŹ½ŗĶ·ÖĒéæöĒótµÄÖµ£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | x”Ł0 | B£® | x”Ł1 | C£® | x”Ł1»ņx”Ł-1 | D£® | x”Ł1ĒŅx”Ł-1 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com