
 分别画出这两个函数的图象
分别画出这两个函数的图象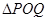 的面积
的面积 科目:初中数学 来源: 题型:
(本题10分)已知△ABC的一条边BC的长为5,另两边AB、AC的长是关于x的一元二次方程![]() 的两个实数根.
的两个实数根.
(1)求证:无论![]() 为何值时,方程总有两个不相等的实数根;
为何值时,方程总有两个不相等的实数根;
(2)当![]() 为何值时,△ABC是以BC为斜边的直角三角形;
为何值时,△ABC是以BC为斜边的直角三角形;
查看答案和解析>>
科目:初中数学 来源: 题型:
 的图像上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点M1在第二象限.
的图像上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点M1在第二象限. ,P点坐标为(1, 0),图中已画出一符合条件的一个正方形PQMN,请你在图中画出符合条件的另一个正方形PQ1M1N1,并写出点M1的坐标;
,P点坐标为(1, 0),图中已画出一符合条件的一个正方形PQMN,请你在图中画出符合条件的另一个正方形PQ1M1N1,并写出点M1的坐标; 
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省海安县曲塘中学附属初级中学九年级上学期期中考试数学卷 题型:解答题
(本题10分)已知△ABC的一条边BC的长为5,另两边AB、AC的长是关于x的一元二次方程 的两个实数根.
的两个实数根.
(1)求证:无论 为何值时,方程总有两个不相等的实数根;
为何值时,方程总有两个不相等的实数根;
(2)当 为何值时,△ABC是以BC为斜边的直角三角形;
为何值时,△ABC是以BC为斜边的直角三角形;
查看答案和解析>>
科目:初中数学 来源:2010年高级中等学校招生全国统一考试数学卷(山东莱芜) 题型:解答题
(本题10分)
已知点P的坐标为(m,0),在x轴上存在点Q(不与P点重合),以PQ为边作正方形PQMN,使点M落在反比例函数y =  的图像上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点M1在第二象限.
的图像上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点M1在第二象限.
(1)如图所示,若反比例函数解析式为y=  ,P点坐标为(1, 0),图中已画出一符合条件的一个正方形PQMN,请你在图中画出符合条件的另一个正方形PQ1M1N1,并写出点M1的坐标;
,P点坐标为(1, 0),图中已画出一符合条件的一个正方形PQMN,请你在图中画出符合条件的另一个正方形PQ1M1N1,并写出点M1的坐标; 
(温馨提示:作图时,别忘了用黑色字迹的钢笔或签字笔描黑喔!)
M1的坐标是 ▲
(2) 请你通过改变P点坐标,对直线M1 M的解析式y﹦kx+b进行探究可得 k﹦ ▲ , 若点P的坐标为(m,0)时,则b﹦ ▲ ;
(3) 依据(2)的规律,如果点P的坐标为(6,0),请你求出点M1和点M的坐标.
查看答案和解析>>
科目:初中数学 来源:2010年高级中等学校招生全国统一考试数学卷(山东莱芜) 题型:解答题
(本题10分)
已知点P的坐标为(m,0),在x轴上存在点Q(不与P点重合),以PQ为边作正方形PQMN,使点M落在反比例函数y =  的图像上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点M1在第二象限.
的图像上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点M1在第二象限.
(1)如图所示,若反比例函数解析式为y=  ,P点坐标为(1, 0),图中已画出一符合条件的一个正方形PQMN,请你在图中画出符合条件的另一个正方形PQ1M1N1,并写出点M1的坐标;
,P点坐标为(1, 0),图中已画出一符合条件的一个正方形PQMN,请你在图中画出符合条件的另一个正方形PQ1M1N1,并写出点M1的坐标;

(温馨提示:作图时,别忘了用黑色字迹的钢笔或签字笔描黑喔!)
M1的坐标是 ▲
(2) 请你通过改变P点坐标,对直线M1 M的解析式y﹦kx+b进行探究可得 k﹦ ▲ , 若点P的坐标为(m,0)时,则b﹦ ▲ ;
(3) 依据(2)的规律,如果点P的坐标为(6,0),请你求出点M1和点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com