
���� ��1������ͼ����x�������������㣬��ú���Ϊ���κ����ҡ���0���ʴ˿ɵõ�����m�IJ���ʽ�飬�Ӷ������m��ȡֵ��Χ��
��2������������ߵĶԳ��ᣬ��n��x��-1ʱ������ͼ��λ�ڶԳ������࣬y��x���������С������x=nʱ��y�����ֵ-3n��Ȼ��x=n��y=-3n������⼴�ɣ�
��3������õ�M�����꣬Ȼ������õ�MP����Բ��ʱ��PM�����ֵ���ʴ˿���õ�P�����꣬�Ӷ��ɵõ�����C2�Ľ���ʽ��
��� �⣺��1���ߺ���ͼ����x�����������㣬
��m��0��[-��2m-5��]2-4m��m-2����0��
��ã�m��$\frac{25}{12}$��m��0��
��m�������������������
��m=2��
�ຯ���Ľ���ʽΪy=2x2+x��
��2�������ߵĶԳ���Ϊx=-$\frac{b}{2a}$=-$\frac{1}{4}$��
��n��x��-1��-$\frac{1}{4}$��a=2��0��
�൱n��x��-1ʱ��y��x���������С��
�൱x=nʱ��y=-3n��
��2n2+n=-3n�����n=-2��n=0����ȥ����
��n��ֵΪ-2��
��3����y=2x2+x=2��x+$\frac{1}{4}$��2-$\frac{1}{8}$��
��M��-$\frac{1}{4}$��-$\frac{1}{8}$����
��ͼ��ʾ��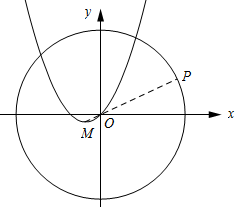
����P��OM���O�Ľ��㴦ʱ��PM�����ֵ��
��ֱ��OM�Ľ���ʽΪy=kx������M���������ã�-$\frac{1}{4}$k=-$\frac{1}{8}$����ã�k=$\frac{1}{2}$��
��OM�Ľ���ʽΪy=$\frac{1}{2}$x��
���P��������x��$\frac{1}{2}$x����
�������ľ��빫ʽ��֪��OP=$\sqrt{{x}^{2}+��\frac{1}{2}x��^{2}}$=$\sqrt{5}$��
��ã�x=2��x=-2����ȥ����
���P��������2��1����
�൱��P���M�������ʱ����C2�Ľ���ʽΪy=2��x-2��2+1��
���� ������Ҫ������Ƕ��κ������ۺ�Ӧ�ã��������ҪӦ��һԪ���η��̸����б�ʽ�����κ�����ͼ������ʣ����ɶ�����Ӧ�ã�����ϵ������һ�κ����Ľ���ʽ���ҳ�PMȡ�����ֵ�������ǽ���Ĺؼ���


 ����������ϵ�д�
����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪Rt��ABC����C=90�㣬DΪBC���е㣬��ACΪֱ���ġ�O��AB�ڵ�E��
��ͼ����֪Rt��ABC����C=90�㣬DΪBC���е㣬��ACΪֱ���ġ�O��AB�ڵ�E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2x•3x=6x | B�� | 3x-2x=x | C�� | ��2x��2=4x | D�� | 6x��2x=3x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1.6��10-4 | B�� | 1.6��10-5 | C�� | 1.6��10-6 | D�� | 16��10-6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3��4֮�� | B�� | 4��5֮�� | C�� | 5��6֮�� | D�� | 6��7֮�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 10 | B�� | 12 | C�� | 14 | D�� | 16 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | 0 | C�� | 1 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
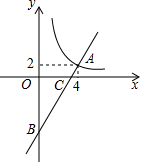 ��ͼ��һ�κ���y=kx+b��ͼ���뷴��������y=$\frac{m}{x}$��ͼ���ڵ�һ�����ڵ�A��4��2������y��ĸ����ύ�ڵ�B����OB=6��
��ͼ��һ�κ���y=kx+b��ͼ���뷴��������y=$\frac{m}{x}$��ͼ���ڵ�һ�����ڵ�A��4��2������y��ĸ����ύ�ڵ�B����OB=6���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com