
 如图,已知Rt△ABC,∠C=90°,D为BC的中点,以AC为直径的⊙O交AB于点E.
如图,已知Rt△ABC,∠C=90°,D为BC的中点,以AC为直径的⊙O交AB于点E.分析 (1)求出∠OED=∠BCA=90°,根据切线的判定得出即可;
(2)求出△BEC∽△BCA,得出比例式,代入求出即可.
解答 (1)证明:
连接OE、EC,
∵AC是⊙O的直径,
∴∠AEC=∠BEC=90°,
∵D为BC的中点,
∴ED=DC=BD,
∴∠1=∠2,
∵OE=OC,
∴∠3=∠4,
∴∠1+∠3=∠2+∠4,
即∠OED=∠ACB,
∵∠ACB=90°,
∴∠OED=90°,
∴DE是⊙O的切线;
(2)解:由(1)知:∠BEC=90°,
∵在Rt△BEC与Rt△BCA中,∠B=∠B,∠BEC=∠BCA,
∴△BEC∽△BCA,
∴$\frac{BE}{BC}$=$\frac{BC}{BA}$,
∴BC2=BE•BA,
∵AE:EB=1:2,设AE=x,则BE=2x,BA=3x,
∵BC=6,
∴62=2x•3x,
解得:x=$\sqrt{6}$,
即AE=$\sqrt{6}$.
点评 本题考查了切线的判定和相似三角形的性质和判定,能求出∠OED=∠BCA和△BEC∽△BCA是解此题的关键.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:填空题
 完全平方式(a+b)2=a2+2ab+b2中,等式右边各项系数依次是1,2,1,那么,(a+b)3,(a+b)4,…(a+b)n展开后的各项系数有什么规律呢?11世纪中叶,我国数学家贾宪给出了直到(a+b)6的系数表(如图),请观察系数表,请写出(a+b)7展开后从左向右第三项的系数21.
完全平方式(a+b)2=a2+2ab+b2中,等式右边各项系数依次是1,2,1,那么,(a+b)3,(a+b)4,…(a+b)n展开后的各项系数有什么规律呢?11世纪中叶,我国数学家贾宪给出了直到(a+b)6的系数表(如图),请观察系数表,请写出(a+b)7展开后从左向右第三项的系数21.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
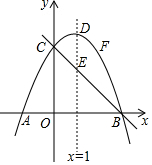 如图,抛物线y=ax2+bx+4(a≠0)与y轴交于C点,与x轴交于A(-2,0)、B两点,抛物线的对称轴直线x=1交抛物线于D点,交直线BC于E点.
如图,抛物线y=ax2+bx+4(a≠0)与y轴交于C点,与x轴交于A(-2,0)、B两点,抛物线的对称轴直线x=1交抛物线于D点,交直线BC于E点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
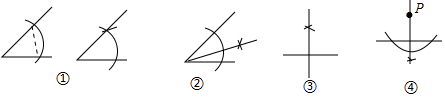
| A. | ① | B. | ② | C. | ③ | D. | ④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 182 | 195 | 201 | 179 | 208 | 204 | 186 | 192 | 210 | 204 |
| 175 | 193 | 200 | 203 | 188 | 197 | 212 | 207 | 185 | 206 |
| 188 | 186 | 198 | 202 | 221 | 199 | 219 | 208 | 187 | 224 |
| 谷粒颗数 | 175≤x<185 | 185≤x<195 | 195≤x<205 | 205≤x<215 | 215≤x<225 |
| 频数 | 3 | 8 | 10 | 6 | 3 |
| 对应扇形 图中区域 | B | D | E | A | C |

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 小明从家到图书馆看报然后返回,他离家的距离y与离家的时间x之间的对应关系如图所示,如果小明在图书馆看报30分钟,那么他离家50分钟时离家的距离为0.3km.
小明从家到图书馆看报然后返回,他离家的距离y与离家的时间x之间的对应关系如图所示,如果小明在图书馆看报30分钟,那么他离家50分钟时离家的距离为0.3km.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com