
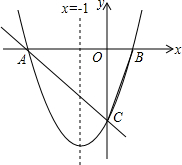
 如图,对称轴为直线x=-1的抛物线y=x2+bx+c与x轴相交于A、B两点,与y轴的交于C点,其中A点的坐标为(-3,0).
如图,对称轴为直线x=-1的抛物线y=x2+bx+c与x轴相交于A、B两点,与y轴的交于C点,其中A点的坐标为(-3,0).分析 (1)首先根据对称轴求出b的值,再根据抛物线y=x2+bx+c过(-3,0)点,求出c的值,抛物线解析式即可求出;
(2)根据平移知识可得B(m+1,0),C(0,m2-2m-3),利用△BOC为等腰直角三角形,得到|m2-2m-3|=(m+1),进而求出m的值.
解答 解:(1)∵抛物线y=x2+bx+c的对称轴为x=-1,
∴-$\frac{b}{2}$=-1,
∴b=2,
∵抛物线y=x2+bx+c过(-3,0)点,
∴9-6+c=0,
∴c=-3,
∴抛物线解析式为y=x2+2x-3;
(2)y=x2+2x-3,
y=(x+1)2-4,
向右平移m个单位后,y=(x+1-m)2-4,
向右平移后B(m+1,0),C(0,m2-2m-3).
①m2-2m-3=-(m+1),解得m=2,m=-1(舍去);
②m2-2m-3=m+1,解得m=4,m=-1(舍去);
综上m的值为2或4.
点评 本题主要考查了二次函数综合题,解答本题的关键是熟练掌握二次函数的性质以及平移的性质,解答(2)问时需要分类讨论,此题难度不大.


科目:初中数学 来源: 题型:解答题
 如图,在直角坐标系中,⊙C过原点O,交x轴于点A(2,0),交y轴于点B(0,$2\sqrt{3}}$).
如图,在直角坐标系中,⊙C过原点O,交x轴于点A(2,0),交y轴于点B(0,$2\sqrt{3}}$).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,抛物线y=ax2+bx+c(a>0)的对称轴是过点(1,0)且平行于y轴的直线,若点P(4,0)在该抛物线上,则4a-2b+c的值为0;当x=-2时,y=4a-2b+c;根据抛物线的对称性可知抛物线与x轴的另一个交点(-2,0).
如图,抛物线y=ax2+bx+c(a>0)的对称轴是过点(1,0)且平行于y轴的直线,若点P(4,0)在该抛物线上,则4a-2b+c的值为0;当x=-2时,y=4a-2b+c;根据抛物线的对称性可知抛物线与x轴的另一个交点(-2,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
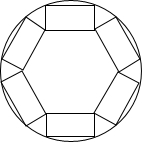 如图为一个半径为4m的圆形广场,其中放有六个宽为1m的长方形临时摊位,这些摊位均有两个顶点在广场边上,另两个顶点紧靠相邻摊位的顶点,则每个长方形摊位的长为$\frac{-\sqrt{3}+3\sqrt{7}}{2}$m.
如图为一个半径为4m的圆形广场,其中放有六个宽为1m的长方形临时摊位,这些摊位均有两个顶点在广场边上,另两个顶点紧靠相邻摊位的顶点,则每个长方形摊位的长为$\frac{-\sqrt{3}+3\sqrt{7}}{2}$m.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在A、B两处之间要修一条笔直的公路,从A地测得公路走向是北偏东46°,A、B两地同时开工,若干天后公路准确接通.
如图,在A、B两处之间要修一条笔直的公路,从A地测得公路走向是北偏东46°,A、B两地同时开工,若干天后公路准确接通.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
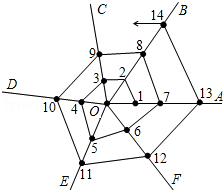 如图,以O为端点画六条射线OA,OB,OC,OD,OE,OF后,再从射线OA上某点开始按逆时针方向依次在各射线上描点并连线,若将各条射线上所描的点依次记为1,2,3,4,5,6,7,8,…那么所描的第2015个点在射线OE上.
如图,以O为端点画六条射线OA,OB,OC,OD,OE,OF后,再从射线OA上某点开始按逆时针方向依次在各射线上描点并连线,若将各条射线上所描的点依次记为1,2,3,4,5,6,7,8,…那么所描的第2015个点在射线OE上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com