
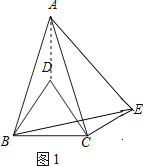
【题目】在△ABC中,AB=AC,∠BAC=α(0°<α<60°),分别以AB、BC为边作等边三角形ABE和等边三角形BCD,连结CE,如图1所示.

(1)直接写出∠ABD的大小(用含α的式子表示);
(2)判断DC与CE的位置关系,并加以证明;
(3)在(2)的条件下,连结DE,如图2,若∠DEC=45°,求α的值.
【答案】(1)∠ABD=30°﹣![]() ∠α;(2)DC与CE垂直;见解析(3)∠α=30°.
∠α;(2)DC与CE垂直;见解析(3)∠α=30°.
【解析】
试题分析:(1)根据等腰三角形的性质得到∠ABC=∠ACB=![]() =90°﹣
=90°﹣![]() ∠α,根据角的和差即可得到结论;
∠α,根据角的和差即可得到结论;
(2)连接AD;根据已知条件得到∠ABD=∠EBC,推出△ABD≌△EBC,根据全等三角形的性质得到∠ADB=∠ECB,证得△ABD≌△ACD,由全等三角形的性质得到∠BAD=∠CAD=![]() ∠α,根据三角形的内角和得到∠BDA=180°﹣∠ABD﹣∠BAD=180°﹣(30°﹣
∠α,根据三角形的内角和得到∠BDA=180°﹣∠ABD﹣∠BAD=180°﹣(30°﹣![]() ∠α )﹣
∠α )﹣![]() ∠α=150°,求得∠BCE=150°,即可得到结论.
∠α=150°,求得∠BCE=150°,即可得到结论.
(3)根据已知条件得到△DEC为等腰三角形,根据等腰直角三角形的性质得到DC=DE=BC,根据三角形的内角和得到∠EBC=15°,即可得到结论.
解:(1)∵AB=AC,∠A=∠α,
∴∠ABC=∠ACB=![]()
=90°﹣![]() ∠α
∠α
∴∠ABD=∠ABC﹣∠ABE
=90°﹣![]() ∠α﹣60°
∠α﹣60°
=30°﹣![]() ∠α;
∠α;
(2)DC与CE垂直;
连接AD;
∵∠ABE=∠DBC=60°,
∴∠ABE﹣∠DBE=∠DBC﹣∠DBE,
即∠ABD=∠EBC,
在△ABD和△EBC中,
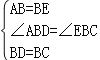 ,
,
∴△ABD≌△EBC,
∴∠ADB=∠ECB,
在△ABD和△ACD中,
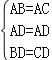 ,
,
∴△ABD≌△ACD,
∴∠BAD=∠CAD=![]() ∠α,
∠α,
∴∠BDA=180°﹣∠ABD﹣∠BAD=180°﹣(30°﹣![]() ∠α )﹣
∠α )﹣![]() ∠α=150°,
∠α=150°,
∴∠BCE=150°,
∵∠BCD=60°,
∴∠DCE=90°,
即DC与CE垂直;
(3)∵∠DCE=90°,
又∵∠DEC=45°,
∴△DEC为等腰三角形,
∴DC=DE=BC,
∵∠BCE=150°,
∴∠EBC=15°,
∵∠EBC=30°﹣![]() ∠α=15°,
∠α=15°,
∴∠α=30°.


科目:初中数学 来源: 题型:
【题目】学习有理数得乘法后,老师给同学们这样一道题目:计算:49![]() ×(﹣5),看谁算的又快又对,有两位同学的解法如下:
×(﹣5),看谁算的又快又对,有两位同学的解法如下:
小明:原式=﹣![]() ×5=﹣
×5=﹣![]() =﹣249
=﹣249![]() ;
;
小军:原式=(49+![]() )×(﹣5)=49×(﹣5)+
)×(﹣5)=49×(﹣5)+![]() ×(﹣5)=﹣249
×(﹣5)=﹣249![]() ;
;
(1)对于以上两种解法,你认为谁的解法较好?
(2)上面的解法对你有何启发,你认为还有更好的方法吗?如果有,请把它写出来;
(3)用你认为最合适的方法计算:19![]() ×(﹣8)
×(﹣8)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的是( )
A.对角线互相平分的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边相等,另一组对边平行的四边形是平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB为直角,∠AOC为锐角,且OM平分∠BOC,ON平分∠AOC.
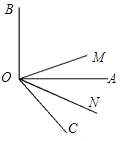
(1)如果∠AOC=50°,求∠MON的度数.
(2)如果∠AOC为任意一个锐角,你能求出∠MON的度数吗?若能,请求出来,若不能,说明为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
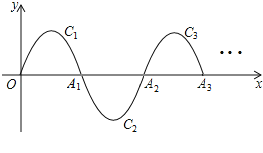
【题目】一段抛物线:y=﹣x(x﹣3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…若P(2015,m)是其中某段抛物线上一点,则m= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)﹣37+(﹣12)﹣(﹣18)﹣13
(2)(﹣1![]() )
)![]() ×
×![]() +(﹣1)5×0
+(﹣1)5×0
(3)﹣|﹣![]() |×|﹣0.25|﹣(﹣5
|×|﹣0.25|﹣(﹣5![]() )
)![]()
(4)﹣14﹣(1﹣0.5)×![]() ×[2﹣(﹣3)2].
×[2﹣(﹣3)2].
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com