
分析 根据菱形的对角线互相垂直平分,可知AO和BO的长,再根据勾股定理求得AB的值,又菱形的四边相等,求出菱形的周长;利用三角函数定义得出tan∠BAO=$\frac{OB}{OA}$=$\frac{7.1}{6.2}$=$\frac{71}{62}$,求出∠BAO的度数,再根据菱形的每一条对角线平分一组对角得出∠BAD=2∠BAO.
解答 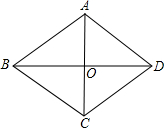 解:如图,已知AC=12.4cm,BD=14.2cm,
解:如图,已知AC=12.4cm,BD=14.2cm,
∵菱形对角线互相垂直平分,
∴AO=6.2cm,BO=7.1cm,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{6.{2}^{2}+7.{1}^{2}}$=$\sqrt{88.85}$≈9.43cm,
∴BC=CD=AD=AB=9.43cm,
∴菱形的周长≈4×9.43≈37.7cm;
∵tan∠BAO=$\frac{OB}{OA}$=$\frac{7.1}{6.2}$=$\frac{71}{62}$,
∴∠BAO≈48°52′,
∴∠BAD=2∠BAO≈97°44′.
点评 本题考查了菱形的两条对角线互相垂直,并且每一条对角线平分一组对角的性质,考查了勾股定理在直角三角形中的运用,考查了三角函数的定义,根据勾股定理求出AB的值是解题的关键.


科目:初中数学 来源: 题型:填空题
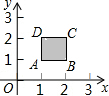 有一种动画程序,屏幕上正方形ABCD是黑色区域(含正方形边界),其中A(1,1)、B(2,1)、C(2,2)、D(1,2),用信号枪沿直线y=2x+b发射信号,当信号遇到黑色区域时,区域便由黑变白,则能够使黑色区域变白的b的取值范围为-3≤b≤0.
有一种动画程序,屏幕上正方形ABCD是黑色区域(含正方形边界),其中A(1,1)、B(2,1)、C(2,2)、D(1,2),用信号枪沿直线y=2x+b发射信号,当信号遇到黑色区域时,区域便由黑变白,则能够使黑色区域变白的b的取值范围为-3≤b≤0.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com