【题目】设
、
是两个任意独立的一位正整数，则点
在抛物线
的上方的概率是（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】
根据a、b是两个任意独立的一位正整数，得出a，b取1～9，然后求出点（a，b）在抛物线y=ax2﹣bx的上方的所有情况，再根据概率公式，即可求出答案．
∵a、b是两个任意独立的一位正整数，∴a，b取1～9，∴代入x=a时，y=a3﹣ba．
∵点（a，b）在抛物线y=ax2﹣bx的上方，∴b﹣y=b﹣a3+ba＞0，当a=1时，b﹣1+b＞0，∴b
，有9个数，b=1，2，3，4，5，6，7，8，9，当a=2时，b﹣8+2b＞0，∴b＞
，有7个数，b=3，4，5，6，7，8，9，当a=3时，b﹣27+3b＞0，∴b＞
，有3个数，b=7，8，9，当a=4时，b﹣64+4b＞0，∴b＞
，有0个数，b在此以上无解，∴共有19个，而总的可能性为9×9=81，∴点（a，b）在抛物线y=ax2﹣bx的上方的概率是
．
故选D．
全优测试卷系列答案
冲刺100分1号卷系列答案科目：初中数学 来源： 题型：
【题目】如图1，在矩形ABCD中，动点E从A出发，沿AB→BC方向运动，当点E到达点C时停止运动，过点E做FE⊥AE，交CD于F点，设点E运动路程为x，FC=y，如图2所表示的是y与x的函数关系的大致图象，当点E在BC上运动时，FC的最大长度是
，则矩形ABCD的面积是_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点D，E分别在AC，AB上，BD与CE相交于点O，已知∠B＝∠C，现添加下面的哪一个条件后，仍不能判定△ABD≌△ACE的是（ ）
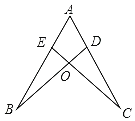
A.AD＝AEB.AB＝ACC.BD＝CED.∠ADB＝∠AEC
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在
中，
，
，边长为
的正方形的一个顶点
在边
上，与另两边分
别交于点
、
，
，将正方形平移，使点保持在上（不与
重合），设
，正方形与重叠部分的面积为
．
求与
的函数关系式并写出自变量的取值范围；
为何值时的值最大？
在哪个范围取值时的值随的增大而减小？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们知道：x2﹣6x＝(x2﹣6x+9)﹣9＝(x﹣3)2﹣9；﹣x2+10＝﹣(x2﹣10x+25)+25＝﹣(x﹣5)2+25，这一种方法称为配方法，利用配方法请解以下各题：
(1)按上面材料提示的方法填空：a2﹣4a＝ ＝ ．﹣a2+12a＝ ＝ ．
(2)探究：当a取不同的实数时在得到的代数式a2﹣4a的值中是否存在最小值？请说明理由．
(3)应用：如图．已知线段AB＝6，M是AB上的一个动点，设AM＝x，以AM为一边作正方形AMND，再以MB、MN为一组邻边作长方形MBCN．问：当点M在AB上运动时，长方形MBCN的面积是否存在最大值？若存在，请求出这个最大值；否则请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在△ABC中，AB＝AC，点D在边BC上，点E在边AC上，且AD＝AE．
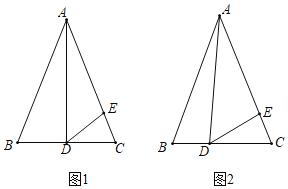
（1）如图1，当AD是边BC上的高，且∠BAD＝30°时，求∠EDC的度数；
（2）如图2，当AD不是边BC上的高时，请判断∠BAD与∠EDC之间的关系，并加以证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校为了解学生的安全意识情况，在全校范围内随机抽取部分学生进行问卷调查，根据调查结果，把学生的安全意识分成“淡薄”、“一般”、“较强”、“很强”四个层次，并绘制成如图9的两幅尚不完整的统计图．
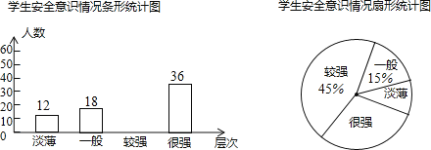
根据以上信息，解答下列问题：
（1）这次调查一共抽取了 名学生；
（2）请将条形统计图补充完整；
（3）分别求出安全意识为“淡薄”的学生占被调查学生总数的百分比、安全意识为“很强”的学生所在扇形的圆心角的度数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠ABC和∠ACB的平分线相交于点G，过点G作EF∥BC交AB于E，交AC于F，过点G作GD⊥AC于D，下列四个结论：
①EF＝BE+CF；②∠BGC＝90°+
∠A；③点G到△ABC各边的距离相等；④设GD＝m，AE+AF＝n，则S△AEF＝mn．其中正确的结论有（ ）
A.①②④B.①③④C.①②③D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
