

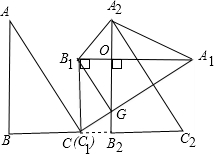
分析 根据题意,在整个图形的变化过程中,BC与四边形A1A2B1G的面积是两个变量设BC=t(1<t<4),四边形A1A2B1G的面积=s,设A1 B1 与 A2B2相交于点O,
可证明△A1 OG∽△A1 B1 C1,得OA2与OG的长即可判定四边形A1A2B1G的面积.
解答 解:如下图所示:
设BC=t(1<t<4),四边形A1A2B1G的面积=s,设 A1 B1 与A2G相交于点O
∵△ABC绕着点C旋转90°与△A1 B1 C1 重合,△ABC向右平移5个格后与△A2B2C2重合
∴A1 B1⊥B1 C${\;}_{{\;}_{1}}$,A1 B1⊥OG,
∴A1 B1∥OG
∴△A1 OG∽△A1 B1 C1
∴$\frac{{A}_{1}{B}_{1}}{{A}_{1}O}=\frac{{B}_{1}{C}_{1}}{OG}$
∴$\frac{OG}{t}=\frac{4-(5-t)}{4}$
∴OG=$\frac{{t}^{2}-t}{4}$
∴s=$\frac{1}{2}$ A1 B1•OA2+$\frac{1}{2}$ A1 B1•OG
又OA2=4-t,A1 B1=4,
∴s=$\frac{1}{2}$×4(4-t+$\frac{{t}^{2}-t}{4}$)
s=$\frac{1}{2}$t2-$\frac{5}{2}$t+8(1<t<4)
∵s=$\frac{1}{2}$t2-$\frac{5}{2}$t+8=$\frac{1}{2}$(t-$\frac{5}{2}$)2+$\frac{39}{8}$(1<t<4)
∴Smin=$\frac{39}{8}$
即:当BC的长为$\frac{5}{2}$是,四边形A1A2B1G的面积最小为$\frac{39}{8}$
点评 本题考查了图形的旋转、平移的性质,解题的关键是分析求出图象在变换过程中变化的量BC与四边形A1A2B1G的面积之间的关系.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 0.25×10-5 | B. | 2.5×10-6 | C. | 25×10-7 | D. | 2.5×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售时段 | 第一周 | 第二周 | |
| 销售数量(台) | A型 | 5 | 10 |
| B型 | 3 | 5 | |
| 销售收入(万元) | 3.98 | 7.4 | |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,已知点A(0,2),B(4,0),C(4,3)三点.
如图,在平面直角坐标系中,已知点A(0,2),B(4,0),C(4,3)三点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在如图所示的正方形网格中,每个小正方形的边长均为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为(-4,5)、(-1,3).
在如图所示的正方形网格中,每个小正方形的边长均为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为(-4,5)、(-1,3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com