
分析 (1)根据绝对值的性质,可化简方程,根据解一元一次方程,可得答案;
(2)根据绝对值的性质,可化简方程,根据解一元一次方程,可得答案.
解答 解:(1)当x<-$\frac{3}{2}$时,原方程等价于2x+3=-8,解得x=-$\frac{11}{2}$;
当x≥-$\frac{3}{2}$时,原方程等价于2x+3=8,解得x=$\frac{5}{2}$;
综上所述,方程|2x+3|=8的解为x=-$\frac{11}{2}$或x=$\frac{5}{2}$.
(2)当x<-$\frac{3}{2}$时,原方程等价于-x-4=1,解得x=-5;
当-$\frac{3}{2}$≤x<1时,原方程等价于3x+2=1,解得x=-$\frac{1}{3}$;
当x≥1时,原方程等价于x+4=1,解得x=-3,(不符合题意,舍);
综上所述,方程:|2x+3|-|x-1|=1的解为x=-5或x=-$\frac{1}{3}$.
点评 本题考查了含绝对值符号的一元一次方程,利用绝对值的性质化简方程是解题关键,要分类讨论,以防遗漏.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
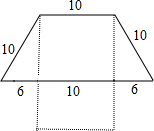 墙上钉着用一根彩绳围成的梯形形状的饰物,如图实线所示(单位:cm).小颖将梯形下底的钉子去掉,并将这条彩绳钉成一个长方形,如图虚线所示.小颖所钉长方形的长、宽各为多少厘米?如果设长方形的长为xcm,根据题意,可得方程为( )
墙上钉着用一根彩绳围成的梯形形状的饰物,如图实线所示(单位:cm).小颖将梯形下底的钉子去掉,并将这条彩绳钉成一个长方形,如图虚线所示.小颖所钉长方形的长、宽各为多少厘米?如果设长方形的长为xcm,根据题意,可得方程为( )| A. | 2(x+10)=10×4+6×2 | B. | 2(x+10)=10×3+6×2 | C. | 2x+10=10×4+6×2 | D. | 2(x+10)=10×2+6×2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 册数 | 0 | 1 | 2 | 3 | 4 |
| 人数 | 3 | 13 | 16 | 17 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com