Question

2．已知抛物线y=ax²+1与x轴交于点A、B（点A在B点左侧），且与直线y=2x+2仅有一个公共点．
（1）求A、B两点的坐标；
（2）如图（1）过B点的直线交y轴负半轴于点P，且交抛物线于另一点C，若S_△APC=3S_△PAB，试求出点P的坐标．
（3）如图（2）在（2）的条件下，若过点P的另一条直线l交抛物线于M、N两点（M在N的左侧），且OM⊥ON，求直线l的解析式．

Answer 1

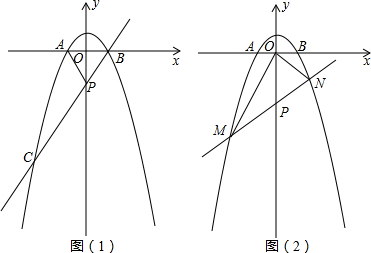
分析 （1）由y=ax²+1直线y=2x+2仅有一个公共点，联立得出的方程ax²-2x-1=0的△=0，可求出a的值，即可得出抛物线的解析式，再令y=0求解即可得出点A，B的坐标；
（2）作CD⊥y轴交y轴于点D，由S_△APC=3S_△PAB，可得CP=3BP，由△POB∽△PDC，可得CD=3OB，OB=1，CD=3，把x=-3代入y=-x²+1，得y=-8，可得C点的坐标，设直线BC的解析式为y=kx+b，把B，C代入可得出k，b的值，进而得出BC的解析式即可得出P点的坐标；
（3）设直线l的解析式为y=kx-2，直线l交抛物线于M、N两点，联立可得M、N两点的坐标，由OM⊥ON，可得tan∠BON=tan∠MOP，利用$\frac{{y}_{1}}{{x}_{1}}$=-$\frac{{x}_{2}}{{y}_{2}}$，可解得k的值，即可得出直线l的解析式．

解答 解：（1）∵y=ax²+1直线y=2x+2仅有一个公共点，
∴ax²+1=2x+2，即ax²-2x-1=0，△=4+4a=0，解得a=-1，
∴抛物线的解析式为：y=-x²+1，
令y=0时，-x²+1=0，解得x=±1，
∴A（-1，0），B（1，0），
（2）如图1，作CD⊥y轴交y轴于点D，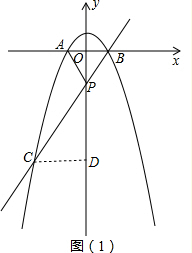

∵S_△APC=3S_△PAB，
∴CP=3BP，
∵△POB∽△PDC，
∴CD=3OB，
∵OB=1，
∴CD=3，把x=-3代入y=-x²+1，得y=-8，
∴C（-3，-8），
设直线BC的解析式为y=kx+b，把B（1，0），C（-3，-8）代入得$\left\{\begin{array}{l}{k+b=0}\\{-3k+b=-8}\end{array}\right.$，解得$\left\{\begin{array}{l}{k=2}\\{b=-2}\end{array}\right.$，
∴直线BC的解析式为y=2x-2，
∴P（0，-2）；
（3）如图2，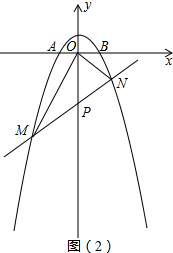

∵P（0，-2），
∴设直线l的解析式为y=kx-2，
∵直线l交抛物线于M、N两点
∴联立得$\left\{\begin{array}{l}{y=kx-2}\\{y=-{x}^{2}+1}\end{array}\right.$，解得$\left\{\begin{array}{l}{{x}_{1}=\frac{-k+\sqrt{{k}^{2}+12}}{2}}\\{{y}_{1}=k•\frac{-k+\sqrt{{k}^{2}+12}}{2}-2}\end{array}\right.$或$\left\{\begin{array}{l}{{x}_{2}=\frac{-k-\sqrt{{k}^{2}+12}}{2}}\\{{y}_{2}=k•\frac{-k-\sqrt{{k}^{2}+12}}{2}-2}\end{array}\right.$，
∵OM⊥ON，
∴tan∠BON=tan∠MOP，
∴$\frac{{y}_{1}}{{x}_{1}}$=-$\frac{{x}_{2}}{{y}_{2}}$，即y₁•y₂=-x₁•x₂，
（k•$\frac{-k+\sqrt{{k}^{2}+12}}{2}$-2）×（k•$\frac{-k-\sqrt{{k}^{2}+12}}{2}$-2）=3，化简得k²=1，解得k=±1，
∴直线l的解析式为y=x-2或直线l的解析式为y=-x-2．

点评 本题主要考查了二次函数综合题，涉及方程判别式，三角形相似，一次函数等知识，解题的关键是利用三角形的面积关系得出点P的坐标．