Question

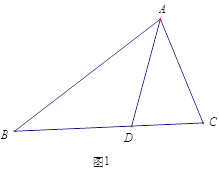
【题目】如图1，△ABC中，AD是∠BAC的角平分线，若AB=AC+CD.那么∠ACB 与∠ABC有怎样的数量关系? 小明通过观察分析，形成了如下解题思路:

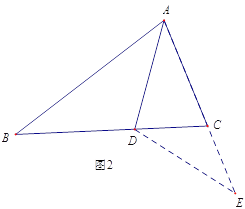
如图2,延长AC到E,使CE=CD,连接DE,由AB=AC+CD,可得AE=AB,又因为AD是∠BAC的平分线，可得△ABD≌△AED,进一步分析就可以得到∠ACB 与∠ABC的数量关系.

(1) 判定△ABD 与△AED 全等的依据是______________(SSS,SAS,ASA,AAS 从其中选择一个);

(2)∠ACB 与∠ABC的数量关系为:___________________

Answer 1

【答案】 SAS ∠ACB =2∠ABC

【解析】试题分析：（1）根据已知以及作法可知可以利用SAS判定△ABD 与△AED 全等；

（2）根据△ABD ≌△AED，可得∠B=∠E，由作法可知CE=CD，从而得∠E=∠CDE，再利用三角形外角的性质即可得∠ACB=2∠ABC.

试题解析：（1）延长AC到E，使CE=CD，连接DE，

∵AB=AC+CD，AE=AC+CE，∴AE=AB，

又∵AD是∠BAC的平分线，∴∠BAD=∠CAD，

又AD是公共边，∴△ABD≌△AED（SAS），

故答案为：SAS；

（2）∵△ABD≌△AED，∴∠B=∠E，

∵CD=CE，∴∠E=∠CDE，

∵∠ACB=∠E+∠CDE，

∴∠ACB=2∠B，

故答案为：∠ACB=2∠B.