
����Ŀ��������ͬһͼ�ε������ͬ��ʾ��ʽ��ͬ������֤��һ�ຬ���߶εĵ�ʽ�����ֽ������ķ������dz�֮Ϊ�������
��1����ͼ1���ڵ���������ABC�У�AB=AC��AC���ϵĸ�Ϊh��M�ǵױ�BC�ϵ�����һ�㣬��M����AB��AC�ľ���ֱ�Ϊh1��h2�����������֤����h1+h2=h��

��2������M��BC�ӳ�����ʱ��h1��h2��h֮��ĵ�����ϵʽ���� ������ֱ��д�����۲���֤����
��3����ͼ2��ƽ��ֱ������ϵ��������ֱ��l1��y=![]() x+3��l2��y=��3x+3����l2�ϵ�һ��M��l1�ľ�����1�������ã�1������2���Ľ��������M�����꣮
x+3��l2��y=��3x+3����l2�ϵ�һ��M��l1�ľ�����1�������ã�1������2���Ľ��������M�����꣮
���𰸡���1������������2��h1��h2=h����3����M������Ϊ��![]() ��2����
��2����![]() ��4����
��4����

�����������������(1)�����ݡ�ABC����������ֲ�ͬ�ļ��㷽���ó������߶�֮��Ĺ�ϵ��(2)�����ݵ�һ��ͬ���ķ����ó��𰸣�(3)�����ȷֱ������A����B�͵�C�����꣬Ȼ�����AB�ij��ȣ��ó���ABCΪ���������Σ�Ȼ��ֵ�M��BC���Ϻ͵�M��CB���ӳ�������������ֱ������M�����꣮
����������⣺(1)����S��ABC=S��ABM+S��AMC��S��ABM=![]() ��AB��ME=
��AB��ME=![]() ��AB��h1��
��AB��h1��
S��AMC=![]() ��AC��MF=
��AC��MF=![]() ��AC��h2�� �֡�S��ABC=
��AC��h2�� �֡�S��ABC=![]() ��AC��BD=
��AC��BD=![]() ��AC��h��
��AC��h��
��![]() ��AC��h=
��AC��h=![]() ��AB��h1+
��AB��h1+![]() ��AC��h2�� ��h1+h2=h��
��AC��h2�� ��h1+h2=h��
(2)��h1��h2=h��
(3)����y=![]() x+3����x=0��y=3����y=0��x=��4����
x+3����x=0��y=3����y=0��x=��4����
A����4��0����B��0��3��ͬ�����C��1��0���� AB=![]() =5��AC=5��
=5��AC=5��
����AB=AC������ABC����������
�ٵ���M��BC����ʱ����h1+h2=h�ã�
1+My=OB��My=3��1=2����������y=��3x+3����ã�Mx=![]() �� ��M��
�� ��M��![]() ��2����
��2����
�ڵ���M��CB�ӳ�����ʱ����h1��h2=h�ã�My��1=OB��My=3+1=4��
��������y=��3x+3����ã�Mx=��![]() �� ��M����
�� ��M����![]() ��4����
��4����
���M������![]() ��2����
��2����![]() ��4����
��4����


 ����ѵ�����⿼ϵ�д�
����ѵ�����⿼ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����P��1�� ��2������x��ԳƵĵ�������ǣ� ��
A.��1�� 2��B.��1�� ��2��C.����1�� 2��D.����2�� 1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����60m��ʾ������60m������ô��������40m�����Ա�ʾΪ�� ��
A. ��20mB. ��40mC. 20mD. 40m
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ֲ���ʵ������ֻ��0.000000076������0.000000076�ÿ�ѧ��������ʾΪ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ABC�У�AD�ǡ�BAC�Ľ�ƽ���ߣ���AB=AC+CD.��ô��ACB ���ABC��������������ϵ? С��ͨ���۲�������γ������½���˼·:
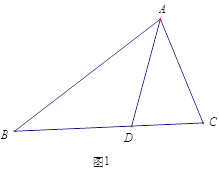
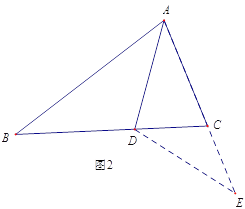
��ͼ2,�ӳ�AC��E,ʹCE=CD,����DE,��AB=AC+CD,�ɵ�AE=AB,����ΪAD�ǡ�BAC��ƽ���ߣ��ɵ���ABD�ա�AED,��һ�������Ϳ��Եõ���ACB ���ABC��������ϵ.
(1) �ж���ABD ����AED ȫ�ȵ�������______________(SSS,SAS,ASA,AAS ������ѡ��һ��);
(2)��ACB ���ABC��������ϵΪ:___________________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�������߾�����ȵĵ��ǡ�ABC�ģ� ����
A.�������ߵĽ���B.�����ߵĴ�ֱƽ���ߵĽ���
C.�����ߵĽ���D.������ƽ���ߵĽ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ȷ����(����)
A. �ҵĴ���ƽ�������ԵĻ�
B. ƽ���ҵ�ֱ�ߴ�ֱ��������
C. ���ҵ��е��ֱ�߱ؾ���Բ��
D. �����Ե����������е����ߴ�ֱƽ���������ҹ�Բ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ҫ�õ�����y=3x+2��ͼ��ֻ�轫����y=3x��ͼ�� ��
A.����ƽ��2����λB.����ƽ��2����λ
C.����ƽ��2����λD.����ƽ��2����λ
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com