
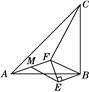
【题目】如图,在△ABC中,∠ABC=90°,BA=BC,△BEF为等腰直角三角形,∠BEF=90°,M为AF的中点,求证:ME=![]() CF.
CF.
【答案】证明见解析.
【解析】试题分析:延长FE到N,使NE=EF,连接AN、BN,判断出△BNF是等腰直角三角形,根据等腰直角三角形的性质可得BN=BF,再求出∠CBF=∠ABN,然后利用“边角边”证明△ABN和△CBF全等,根据全等三角形对应边相等可得AN=CF,再根据三角形的中位线平行于第三边并且等于第三边的一半可得ME=![]() AN,从而得到ME=
AN,从而得到ME=![]() CF.
CF.
试题解析:如图,延长FE至N,使EN=EF,连接BN,AN.易得ME=![]() AN.
AN.
∵EF=EN,∠BEF=90°,∴BE垂直平分FN.∴BF=BN.
∴∠BNF=∠BFN.∵△BEF为等腰直角三角形,∠BEF=90°,
∴∠BFN=45°.∴∠BNF=45°,
∴∠FBN=90°,即∠FBA+∠ABN=90°.
又∵∠FBA+∠CBF=90°,
∴∠CBF=∠ABN.在△BCF和△BAN中,
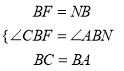
∴△BCF≌△BAN.
∴CF=AN.∴ME=![]() AN=
AN=![]() CF.
CF.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案科目:初中数学 来源: 题型:
【题目】为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 | 成绩x分 | 频数(人数) |
第1组 | 25≤x<30 | 4 |
第2组 | 30≤x<35 | 8 |
第3组 | 35≤x<40 | 16 |
第4组 | 40≤x<45 | a |
第5组 | 45≤x<50 | 10 |
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
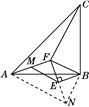
【题目】如图,在△ABC中,∠ACB=90°,点D,E在AB上,且AF垂直平分CD,BG垂直平分CE.(1)求∠ECD的度数;(2)若∠ACB为α,则∠ECD的度数能否用含α的式子来表示.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.
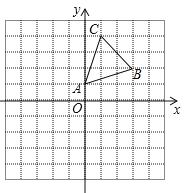
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)将△A1B1C1沿x轴方向向左平移3个单位后得到△A2B2C2,写出顶点A2,B2,C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
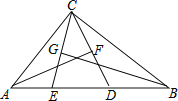
【题目】如图,在△ABC中,AB=BC,AD⊥BC于点D,点E为AC中点且BE平分∠ABD,连接BE交AD于点F,且BF=AC,过点D作DG∥AB,交AC于点G.
求证:
(1)∠BAD=2∠DAC
(2)EF=EG.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有4个黑球、2个白球,每个球除颜色外都相同,从中任意摸出3个球,下列事件为必然事件的是( )
A.至少有1个球是黑球
B.至少有1个球是白球
C.至少有2个球是黑球
D.至少有2个球是白球
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com