
【题目】为了了解江城中学学生的身高情况,随机对该校男生、女生的身高进行抽样调查,已知抽取的样本中,男生、女生的人数相同,根据所得数据绘制成如下所示的统计表和如图所示的统计图.
组别 | 身高(cm) |
A | x<150 |
B | 150≤x<155 |
C | 155≤x<160 |
D | 160≤x<165 |
E | x≥165 |
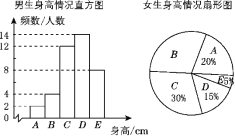
根据图表中提供的信息,回答下列问题:
(1)女生身高在B组的有________人;
(2)在样本中,身高在150≤x<155之间的共有________人,身高人数最多的在________组(填组别序号);
(3)已知该校共有男生500人,女生480人,请估计身高在155≤x<165之间的学生有多少人.
科目:初中数学 来源: 题型:
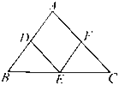
【题目】如图,在![]() 中,点
中,点![]() 分别是
分别是![]() 的中点,则下列四个判断中不一定正确的是()
的中点,则下列四个判断中不一定正确的是()
A. 四边形![]() 一定是平行四边形
一定是平行四边形
B. 若![]() ,则四边形
,则四边形![]() 是矩形
是矩形
C. 若四边形![]() 是菱形,则
是菱形,则![]() 是等边三角形
是等边三角形
D. 若四边形![]() 是正方形,则
是正方形,则![]() 是等腰直角三角形
是等腰直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解本校学生平均每天的课外做作业的时间情况,随机抽取部分学生进行问卷调查,并将调查的结果分为A、B、C、D四个等级(设做作业时间为t小时,A:t<1;B:1≤t<1.5;C:1.5≤t<2;D:t≥2)根据调查结果绘成了如下两幅不完整的统计图.
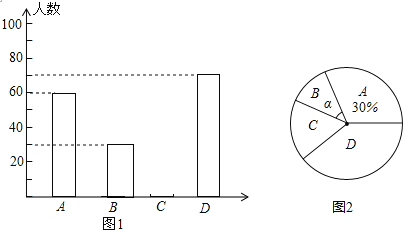
请根据图中信息,解答下列问题:
(1)本次调查中,抽取的学生人数是 ;
(2)图2中α的度数是 ,并补全图1条形统计图;
(3)该校共有2800名学生名,请估计作业时间不少于2小时的人数为 ;
(4)在此次调查中,甲班有2人平均每天的作业时间超过2小时,乙班有3名学生平均每天作业时间超过2小时,现从这5人中选取2人参加座谈会,请用树状图或列表的方法,求出“所选的2人来自不同班级”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数的图象经过![]() ,
,![]() 两点.
两点.
(1)求这个一次函数的解析式;
(2)试判断点![]() 是否在这个一次函数的图象上;
是否在这个一次函数的图象上;
(3)求此函数图象与![]() 轴,
轴,![]() 轴围成的三角形的面积.
轴围成的三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,等边△OAB的顶点B的坐标为(2,0),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′A′B′的位置,此时点A′的横坐标为3,则点B′的坐标为( )
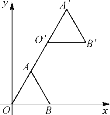
A. (4,2![]() ) B. (3,3) C. (4,3) D. (3,2)
) B. (3,3) C. (4,3) D. (3,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
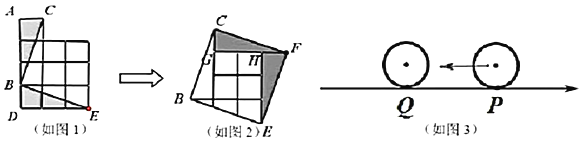
【题目】将如图1中的边长为1个单位长度的10个小正方形,沿![]() 、
、![]() 剪开,后把阴影部分补到如图2三角形
剪开,后把阴影部分补到如图2三角形![]() 与三角形
与三角形![]() 位置中,拼成了一个大正方形,大正方形的边长设为
位置中,拼成了一个大正方形,大正方形的边长设为![]() ;如图3将直径为1的圆放在点
;如图3将直径为1的圆放在点![]() 处,
处,![]() 对应的数位
对应的数位![]() ,将圆周沿数轴向左边滚动一周到
,将圆周沿数轴向左边滚动一周到![]() 点,
点,![]() 对应数为
对应数为![]() ,请完成下面问题:
,请完成下面问题:
(1)求出![]() 与
与![]() 的值.
的值.
(2)化简求值:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
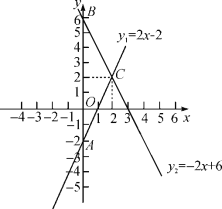
【题目】如图,直线y1=2x-2的图像与y轴交于点A,直线y2=-2x+6的图像与y轴交于点B,两者相交于点C.
(1)方程组![]() 的解是______;
的解是______;
(2)当y1>0与y2>0同时成立时,x的取值范围为_____;
(3)求△ABC的面积;
(4)在直线y1=2x-2的图像上存在异于点C的另一点P,使得△ABC与△ABP的面积相等,请求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市居民生活用水实行“阶梯水价”收费,具体收费标准见下表:
每户每月用水量 | 水的价格(单位:元/吨) |
不超过20吨的部分 | 1.6 |
超过20吨且不超过30吨的部分 | 2.4 |
超过30吨的部分 | 3.3 |
例:甲用户1月份用水25吨,应缴水费![]() (元).
(元).
(1)若乙用户1月份用水10吨,则应缴水费________元;
(2)若丙用户1月份应缴水费62.6元,则用水________吨;.
(3)若丁用户1、2月份共用水60吨(1月份用水量超过了2月份),设2月份用水![]() 吨,求丁用户1、2月份各应缴水费多少元.(用含
吨,求丁用户1、2月份各应缴水费多少元.(用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm,动点P从点A出发沿AD方向向点D以1cm/s的速度运动,动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动.点P、Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.
(1)经过多长时间,四边形PQCD是平行四边形?
(2)经过多长时间,四边形PQBA是矩形?
(3)经过多长时间,当PQ不平行于CD时,有PQ=CD.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com