Question

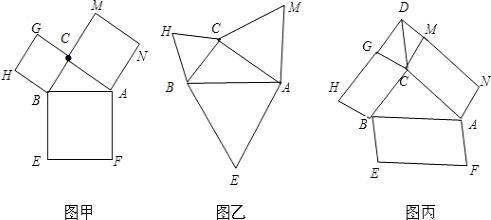
如图甲,正方形ABCD的边长为2,点M是BC的中点,P是线段MC上的一个动点(不运动至M,C),以AB为直径作⊙O,过点P的切线交AD于点F,切点为E。

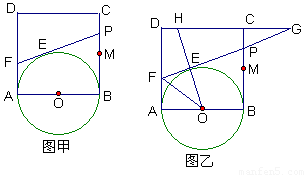
(1)求四边形CDFP的周长；(3分)

(2)请连结OF,OP,求证：OF⊥OP；(4分)

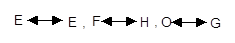(3)延长DC,FP相交于点G,连结OE并延长交直线DC于H(如图乙).是否存在点P

使△EFO∽△EHG(其对应关系是                              )?如果存在,试求此时的BP的长；如果不存在,请说明理由。(5分)

 

Answer 1

【答案】

（1）6（2）证明见解析（3）存在，

【解析】解：(1)∵四边形ABCD是正方形    ∴∠A=∠B=Rt∠  ∴AF、BP都是⊙O的切线  (1分)

        又∵PF是⊙O的切线   ∴EF=FA,PE=PB   ∴四边形CDFP的周长为AD+DC+CB=2×3=6 (3分)

        (2)∴连结OE,∵PF是⊙O的切线  ∴OE⊥PF .

在Rt⊿AOF和Rt⊿EOF中∵AO=EO,OF=OF  ∴Rt⊿AOF∽Rt⊿EOF∴∠AOF=∠EOF(5分)

   同理∠BOP=∠EOP  ∴∠EOF+∠EOP=1/2×180°=90°∴∠EOP=90°即OF⊥OP   (7分)

(3)存在(如果这一步不写,但下面各步骤都正确,不扣分)  (8分)

∵∠EOF=∠AOF  ∴∠EHG=∠AOE=2∠EOF,

∴当∠EHG=∠AOE=2∠EOF,即∠EOF=30°时   Rt⊿EOF∽Rt⊿EHG   (10分)

此时∠EOF=30°,∠BOP=∠EOP=90°－30°=60°

∴BP=OB·tan60°=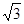  (12分)

（1）根据切线的性质，将所求四边形CDFP的边转化为已知正方形ABCD的边，即可求得；

（2）连结OE，根据切线的性质和相似三角形，求得∠EOP=90°，即可求得OF⊥OP；

（3）要△EFO∽△EHG，必须∠EHG=∠EFO=2∠EOF=60°，在直角△OBP中，由正切定理可求出BP的长．