
 的距离AC.(结果精确到0.1km)(
的距离AC.(结果精确到0.1km)(| 3 |
| AF |
| AB |
| ||
| 2 |
| 3 |
| 3 |
| AE |
| AC |
| AE |
| sin30° |
| 3 |
| 3 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 的距离AC.(结果精确到0.1km)(
的距离AC.(结果精确到0.1km)(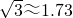 )
)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
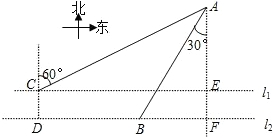
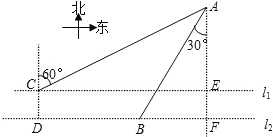
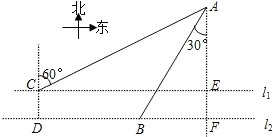 如图,在水上治安指挥塔A西侧两条航线l1、l2上有两艘巡逻艇B与C(C所在航线靠近A),直线l1、l2间的距离CD=
如图,在水上治安指挥塔A西侧两条航线l1、l2上有两艘巡逻艇B与C(C所在航线靠近A),直线l1、l2间的距离CD= km,点B在点A的南偏西30°方向上,且AB=6km,A在C的北偏东60°方向上.求:
km,点B在点A的南偏西30°方向上,且AB=6km,A在C的北偏东60°方向上.求:查看答案和解析>>
科目:初中数学 来源:江苏模拟题 题型:解答题
 )
) 
查看答案和解析>>
科目:初中数学 来源:2010年江苏省南京市溧水县中考数学二模试卷(解析版) 题型:解答题
 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com