135° 128°
分析:①根据角平分线的定义得到∠OBC=

∠ABC=20°,∠OCB=

∠ACB=25°;然后由△OBC的内角和是180度来求∠BOC的度数;
②由△ABC的内角和定理求得∠ABC+∠ACB=104°,则∠BOC=180°-

(∠ABC+∠ACB);
③利用①中的∠BOC=180°-

(∠ABC+∠ACB),以及△ABC的内角和定理求得∠BOC=180°-

(∠ABC+∠ACB)=180°-

(180°-∠A,)=90°+

∠A.
解答:①∵∠ABC=40°,∠ACB=50°,∠ABC、∠ACB的平分线相交于点O,
∴∠OBC=

∠ABC=20°,∠OCB=

∠ACB=25°.
又∵∠BOC+∠OBC+∠OCB=180°,
∴∠BOC=180°-

(∠ABC+∠ACB)=135°.
故填:135°;
②∵在△ABC中,∠A=76°,
∴∠ABC+∠ACB=104°,
∴由①知,∠BOC=180°-

(∠ABC+∠ACB)=128°.
故填:128°;
③∠BOC=90°+

∠A,理由如下
∠BOC=180°-

(∠ABC+∠ACB)=180°-

(180°-∠A)=90°+

∠A.
点评:本题考查了三角形内角和定理.三角形的内角和等于180°.

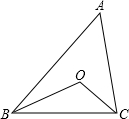 如图,在△ABC中,∠ABC、∠ACB的平分线相交于点O.
如图,在△ABC中,∠ABC、∠ACB的平分线相交于点O. ∠ABC=20°,∠OCB=
∠ABC=20°,∠OCB= ∠ACB=25°;然后由△OBC的内角和是180度来求∠BOC的度数;
∠ACB=25°;然后由△OBC的内角和是180度来求∠BOC的度数; (∠ABC+∠ACB);
(∠ABC+∠ACB); (∠ABC+∠ACB),以及△ABC的内角和定理求得∠BOC=180°-
(∠ABC+∠ACB),以及△ABC的内角和定理求得∠BOC=180°- (∠ABC+∠ACB)=180°-
(∠ABC+∠ACB)=180°- (180°-∠A,)=90°+
(180°-∠A,)=90°+ ∠A.
∠A. ∠ABC=20°,∠OCB=
∠ABC=20°,∠OCB= ∠ACB=25°.
∠ACB=25°. (∠ABC+∠ACB)=135°.
(∠ABC+∠ACB)=135°. (∠ABC+∠ACB)=128°.
(∠ABC+∠ACB)=128°. ∠A,理由如下
∠A,理由如下 (∠ABC+∠ACB)=180°-
(∠ABC+∠ACB)=180°- (180°-∠A)=90°+
(180°-∠A)=90°+ ∠A.
∠A.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为