
 如图,在边长为l的正方形组成的网络中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O逆时针旋转90°后得到△A1OB1,△AOB关于x轴对称的图形为△A2OB2.
如图,在边长为l的正方形组成的网络中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O逆时针旋转90°后得到△A1OB1,△AOB关于x轴对称的图形为△A2OB2.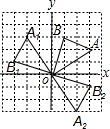 解:(1)B1(-3,1),M(0,0);
解:(1)B1(-3,1),M(0,0);| 12+32 |
| 10 |
90•π•
| ||
| 180 |
| ||
| 2 |
90•π•(
| ||
| 360 |
| 5 |
| 2 |


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
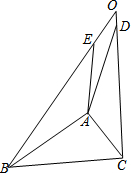 如图,AB、AD是以AB为边向△ABC向外所作正n边形的一组邻边;AC、AE是以AC为边向△ABC外所作正n边形的一组邻边,BE、CD的延长线相交于点O.
如图,AB、AD是以AB为边向△ABC向外所作正n边形的一组邻边;AC、AE是以AC为边向△ABC外所作正n边形的一组邻边,BE、CD的延长线相交于点O.查看答案和解析>>
科目:初中数学 来源: 题型:
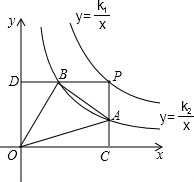 两个反比例函数y=
两个反比例函数y=| k1 |
| x |
| k2 |
| x |
| k1 |
| x |
| k2 |
| x |
| k2 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
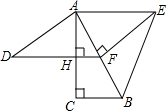 如图,四边形ADFE是平行四边形,EF⊥AF,AH⊥DF,垂足为H,∠FAH=30°,延长AF到点B,使AF=FB,过点B作AH延长线的垂线,垂足为C,连接BE.
如图,四边形ADFE是平行四边形,EF⊥AF,AH⊥DF,垂足为H,∠FAH=30°,延长AF到点B,使AF=FB,过点B作AH延长线的垂线,垂足为C,连接BE.查看答案和解析>>
科目:初中数学 来源: 题型:
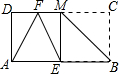 已知:如图,在矩形ABCD中,AB=10,AD=5,将矩形ABCD折叠,使点C落在边AB上的E处,折痕交DC边于点M,点F在DM上运动,当△AEF是腰长为5的等腰三角形时,EF的长为
已知:如图,在矩形ABCD中,AB=10,AD=5,将矩形ABCD折叠,使点C落在边AB上的E处,折痕交DC边于点M,点F在DM上运动,当△AEF是腰长为5的等腰三角形时,EF的长为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com