
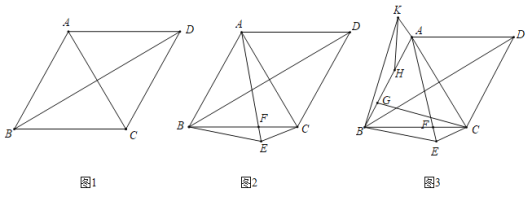
【题目】如图,四边形![]() 中,
中,![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() .
.
(1)如下图,求证:四边形![]() 是菱形;
是菱形;
(2)如下图,点![]() 为四边形
为四边形![]() 外一点,连接
外一点,连接![]() 、
、![]() 、
、![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() ,求证:
,求证:![]() ;
;
(3)如下图,在(2)的条件下,![]() ,点
,点![]() 为
为![]() 上一点,连接
上一点,连接![]() ,点
,点![]() 为
为![]() 延长线上一点,
延长线上一点,![]() ,连接
,连接![]() ,
,![]() 为
为![]() 上一点,连接
上一点,连接![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
【答案】(1)见详解;(2)见详解;(3)6![]() .
.
【解析】
(1)首先证明AB=BC,AB=AD,推出AD=BC,可证四边形ABCD是平行四边形即可解决问题.
(2)欲证明AE=AC,只要证明∠ACE=∠AEC即可.
(3)如图3中,作KJ⊥BA交BA的延长线于J,CI⊥AB于I,设BD交AC于O.首先证明△ABC是等边三角形,易知BO⊥AC,CJ⊥AB,推出BO=CJ,因为S△BCG=![]() BGCI,S△ABK=
BGCI,S△ABK=![]() AKBO,由BG=AK,CI=BO,推出S△BCG=S△ABK,推出S△BCG-S△AKH=S△ABK-S△AKH=S△BHK=
AKBO,由BG=AK,CI=BO,推出S△BCG=S△ABK,推出S△BCG-S△AKH=S△ABK-S△AKH=S△BHK=![]() BHKJ,再证明JK=
BHKJ,再证明JK=![]() AK=
AK=![]() BG即可解决问题.
BG即可解决问题.
(1)证明:如图1中,
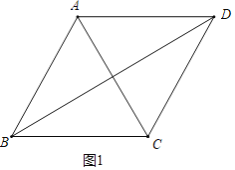
∵AC平分∠BAD,
∴∠CAB=∠CAD,
∵AD∥BC,
∴∠CAD=∠ACB,∠ADB=∠DBC,
∴∠CAB=∠ACB,
∴AB=CB,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABD=∠ADB,
∴AB=AD,
∴AD=BC,
∵AD∥BC,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴四边形ABCD是菱形.
(2)证明:如图2中,
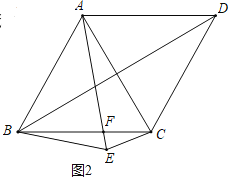
∵BA=BC,
∴∠BAC=∠BCA,
∵∠AFC=2∠AEC-∠BAC,
∴∠AFC+∠ACB=2∠AEC,
∵∠CAF+∠AFC+∠ACB=180°,∠CAE+∠AEC+∠ACE=180°,
∴∠AFC+∠ACB=∠AEC+∠ACE=2∠AEC,
∴∠ACE=∠AEC,
∴AE=AC.
(3)解:如图3中,作KJ⊥BA交BA水电延长线于J,CI⊥AB于I,设BD交AC于O.
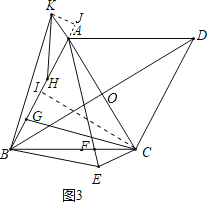
∵AB=AE=AC,
∴△BCE的外接圆的圆心为A,
∵∠BEC=150°,
∴∠EBC+∠BCE=30°,
∵∠EAC=2∠EBC,∠EAB=2∠BCE,
∴∠BAC=2(∠EBC+∠BCE)=60°,
∵BA=BC,
∴△ABC是等边三角形,BO⊥AC,CJ⊥AB,
∴BO=CJ,
∵S△BCG=![]() BGCI,S△ABK=
BGCI,S△ABK=![]() AKBO,
AKBO,
∵BG=AK,CI=BO,
∴S△BCG=S△ABK,
∴S△BCG-S△AKH=S△ABK-S△AKH=S△BHK=![]() BHKJ,
BHKJ,
在Rt△AKJ中,∵∠KAJ=∠BAC=60°,
∴KJ=AKsin60°=![]() AK=
AK=![]() BG,
BG,
∴S△BCG-S△AKH=![]() BHKJ=
BHKJ=![]() BH
BH![]() BG=
BG=![]() BHBG=
BHBG=![]() ×24=6
×24=6![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() 的平分线交
的平分线交![]() 于点E,交
于点E,交![]() 的延长线于F,以
的延长线于F,以![]() 为邻边作平行四边形
为邻边作平行四边形![]() 。
。
(1)证明平行四边形![]() 是菱形;
是菱形;
(2)若![]() ,连结
,连结![]() ,①求证:
,①求证:![]() ;②求
;②求![]() 的度数;
的度数;
(3)若![]() ,
,![]() ,
,![]() ,M是
,M是![]() 的中点,求
的中点,求![]() 的长。
的长。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为平行四边形ABCD边AD上一点,E,F分别为PB,PC的中点,△PEF,△PDC,△PAB的面积分别为S、S1、S2 , 若S=2,则S1+S2=( )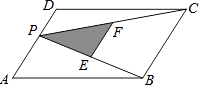
A.4
B.6
C.8
D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向依次不断地移动,每次移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),……,那么点A2019的坐标为( )
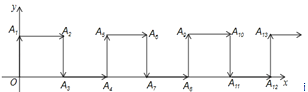
A.(1008,1)B.(1009,1)C.(1009,0)D.(1010,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点![]() 、
、![]() 、
、![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,
,![]() .若点
.若点![]() 从
从![]() 点出发,沿
点出发,沿![]() 轴正方向以每秒1个单位长度的速度向
轴正方向以每秒1个单位长度的速度向![]() 点移动,连接
点移动,连接![]() 并延长到点
并延长到点![]() ,使
,使![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() .若点
.若点![]() 在移动的过程中,使
在移动的过程中,使![]() 成为直角三角形,则点
成为直角三角形,则点![]() 的坐标是__________.
的坐标是__________.
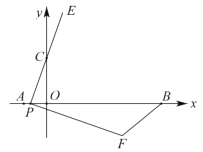
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市经济技术开发区某智能手机有限公司接到生产300万部智能手机的订单,为了尽快交货,增开了一条生产线,实际每月生产能力比原计划提高了50%,结果比原计划提前5个月完成交货,求每月实际生产智能手机多少万部.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=kx+b的图象经过A(﹣2,﹣1),B(1,3)两点,并且交x轴于点C,交y轴于点D.
(1)求该一次函数的解析式;
(2)求△AOB的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com