
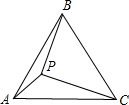
 点P是等边△ABC内一点,且PA=2,
点P是等边△ABC内一点,且PA=2, ,PC=4,求∠APB的度数.(友情提示:将△APC绕A逆时针旋转60°得到△AP′B,连接PP′)
,PC=4,求∠APB的度数.(友情提示:将△APC绕A逆时针旋转60°得到△AP′B,连接PP′) 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
 得△ADC,连接OD.
得△ADC,连接OD.查看答案和解析>>
科目:初中数学 来源: 题型:
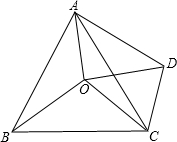
 18、如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
18、如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.查看答案和解析>>
科目:初中数学 来源: 题型:
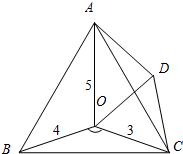 28、如图,点O是等边△ABC内一点,且OA=5,OB=4,OC=3,将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OD,回答下列问题:
28、如图,点O是等边△ABC内一点,且OA=5,OB=4,OC=3,将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OD,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
 得到线段CD,连接OD、AD.
得到线段CD,连接OD、AD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com