练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    请阅读下列及其证明过程，并回答所提出的问题，
    如图，已知P为⊙O外一点，PA、PB为⊙O的切线，A和B是切点，BC是直径。求证：AC∥OP。
    证明：连接AB，交OP于点D，
    ∵PA、PB切⊙O于A、B，
    ∴PA=PB，∠1=∠2；
    ∴PD⊥AB，
    ∴∠3=90°；
    ∵________，（*）
    ∴∠4=90°，
    ∴∠3=∠4，
    ∴AC∥OP，
    （1）在（*）处的横线上补上应填的条件；
    （2）上述证明过程中用到的定理名称或定理的具体内容是（只要求写出两个）。
    解：（1）BC是⊙O的直径；
    （2）切线长定理；等腰三角形顶角的平分线垂直平分底边；直径所对的圆周角是直角；内错角相等，两直线平行。
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    22、我们知道，两边及其中一边的对角分别对应相等的两个三角形不一定全等．那么在什么情况下，它们会全等？
    （1）阅读与证明：
    对于这两个三角形均为直角三角形，显然它们全等．
    对于这两个三角形均为钝角三角形，可证它们全等（证明略）．
    对于这两个三角形均为锐角三角形，它们也全等，可证明如下：
    已知：△ABC、△A1B1C1均为锐角三角形，AB=A1B1，BC=B1Cl，∠C=∠Cl．
    求证：△ABC≌△A1B1C1．
    （请你将下列证明过程补充完整．）
    证明：分别过点B，B1作BD⊥CA于D，
    B1D1⊥C1A1于D1．
    则∠BDC=∠B1D1C1=90°，
    ∵BC=B1C1，∠C=∠C1，
    ∴△BCD≌△B1C1D1，
    ∴BD=B1D1．
    （2）归纳与叙述：
    由（1）可得到一个正确结论，请你写出这个结论．

    查看答案和解析>>

    科目：初中数学 来源：2012年人教版八年级上第十一章全等三角形第二节全等三角形的判定练习卷（解析版） 题型：解答题

    我们知道，两边及其中一边的对角分别对应相等的两个三角形不一定全等. 那么在什么情况下，它们会全等?

    （1）阅读与证明：

    对于这两个三角形均为直角三角形，显然它们全等.

    对于这两个三角形均为钝角三角形，可证它们全等（证明略）.

    对于这两个三角形均为锐角三角形，它们也全等，可证明如下：

    已知：△ABC、△A1B1C1均为锐角三角形，AB＝A1B1，BC＝B1C1，∠C＝∠C1.

    求证：△ABC≌△A1B1C1. （请你将下列证明过程补充完整）

    证明：分别过点B，B1作BD⊥CA于D，B1D1⊥C1A1于D1.

    则∠BDC＝∠B1D1C1＝90°，

    ∵BC＝B1C1，∠C＝∠C1，

    ∴△BCD≌△B1C1D1，

    ∴BD＝B1D1.

    ______________________________。

    （2）归纳与叙述：

    由（1）可得到一个正确结论，请你写出这个结论.

     

     

     

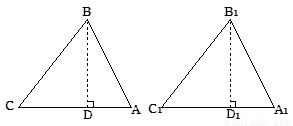
    查看答案和解析>>

    科目：初中数学 来源：同步题 题型：解答题

    我们知道，两边及其中一边的对角分别对应相等的两个三角形不一定全等，那么在什么情况下，它们会全等？
    （1）阅读与证明：对于这两个三角形均为直角三角形，显然它们全等，对于这两个三角形均为钝角三角形，可证它们全等（证明略）对于这两个三角形均为锐角三角形，它们也全等，
    可证明如下：
    已知：如图，△ABC，△A1B1C1均为锐角三角形，AB=A1B1，BC=B1C1，∠C=∠C1。
    求证：△ABC≌△A1B1C1。（请你将下列证明过程补充完整）
    证明：分别过点B，B1作BD⊥CA于D，B1D1⊥C1A1于D1，则∠BDC=∠B1D1C1=90°
    ∵BC=B1C1，∠C=∠C1
    ∴△BCD≌△B1C1D1，
    ∴BD=B1D1，
    ________________，
    ________________；
    （2）归纳与叙述：由（1）可得到一个正确结论，请你写出这个结论。

    查看答案和解析>>

    科目：初中数学 来源：期中题 题型：解答题

    我们知道，两边及其中一边的对角分别对应相等的两个三角形不一定全等。那么在什么情况下，它们会全等？
    （1）阅读与证明：
    对于这两个三角形均为直角三角形，显然它们全等。
    对于这两个三角形均为钝角三角形，可证它们全等（证明略）。
    对于这两个三角形均为锐角三角形，它们也全等，可证明如下：
    已知：△ABC、△A1B1C1均为锐角三角形，AB=A1B1，BC=B1C1，∠C=∠C1。
    求证：△ABC≌△A1B1C1。（请你将下列证明过程补充完整）

    证明：分别过点B，B1作BD⊥CA于D，B1D1⊥C1A1于D1。
    则∠BDC=∠B1D1C1=90°，
    ∵BC=B1C1，∠C=∠C1，
    ∴△BCD≌△B1C1D1，
    ∴BD=B1D1
    （2）归纳与叙述：由（1）可得到一个正确的结论，请你写出这个结论。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    我们知道，两边及其中一边的对角分别对应相等的两个三角形不一定全等．那么在什么情况下，它们会全等?

    (1)阅读与证明：

    对于这两个三角形均为直角三角形，显然它们全等．

    对于这两个三角形均为钝角三角形，可证它们全等(证明略)．

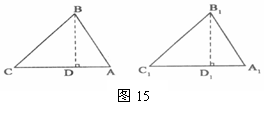
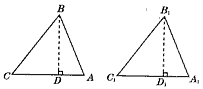
    对于这两个三角形均为锐角三角形，它们也全等，可证明如下：

    已知：△ABC、△A1B1C1均为锐角三角形，AB=A1B1，BC=B1Cl，∠C=∠Cl．

    求证：△ABC≌△A1B1C1．(请你将下列证明过程补充完整)

    证明：分别过点B，B1作BD⊥CA于D，B1 D1⊥C1 A1于D1．则∠BDC=∠B1D1C1=900，

    ∵BC=B1C1，∠C=∠C1，∴△BCD≌△B1C1D1，∴BD=B1D1．

    (2)归纳与叙述： 由(1)可得到一个正确结论，请你写出这个结论．

    查看答案和解析>>

    同步练习册答案