
分析 ①根据一次函数图象与几何变换,在2x+1的后面加3即可得出结论;
②根据一次函数图象与几何变换,将x换成x-3,整理后即可得出结论;
③根据一次函数图象与几何变换,将y换成-y,整理后即可得出结论;
④根据一次函数图象与几何变换,将x换成-x即可得出结论.
解答 解:①将直线y=2x+1向上平移3个单位,所得的直线解析式为y=2x+1+3=2x+4.
故答案为:y=2x+4;
②将直线y=2x+1向右平移3个单位,所得的直线解析式为y=2(x-3)+1=2x-5.
故答案为:y=2x-5;
③将直线y=2x+1作关于x轴对称,所得的解析式为-y=2x+1,
整理得:y=-2x-1.
故答案为:y=-2x-1;
④将直线y=2x+1作关于y轴对称,所得的直线解析式为y=2×(-x)+1=-2x+1.
故答案为:y=-2x+1.
点评 本题考查了一次函数图象与几何变换,熟练掌握一次函数图象与几何变换是解题的关键.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
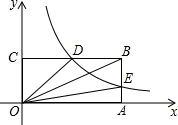 如图,在平面直角坐标系中,点O为坐标系原点,矩形OABC的边OA,OC分别在x轴和y轴上,其中OA=6,OC=3,已知反比例函数y=$\frac{k}{x}$(x>0)的图象经过BC边上的中点D,交AB于点E
如图,在平面直角坐标系中,点O为坐标系原点,矩形OABC的边OA,OC分别在x轴和y轴上,其中OA=6,OC=3,已知反比例函数y=$\frac{k}{x}$(x>0)的图象经过BC边上的中点D,交AB于点E查看答案和解析>>
科目:初中数学 来源: 题型:解答题
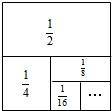 利用图形来表示数量或数量关系,也可以利用数量或数量关系来描述图形特征或图形之间的关系,这种思想方法称为数形结合.我们刚学过的第9章《整式乘法与因式分解》就很好地体现了这一思想方法,你能利用数形结合的思想解决下列问题吗?
利用图形来表示数量或数量关系,也可以利用数量或数量关系来描述图形特征或图形之间的关系,这种思想方法称为数形结合.我们刚学过的第9章《整式乘法与因式分解》就很好地体现了这一思想方法,你能利用数形结合的思想解决下列问题吗?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com