
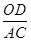 =
= 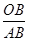 ,即
,即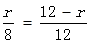 解得:
解得: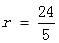
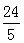 ………………………4分
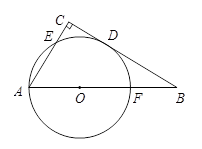
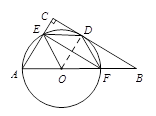
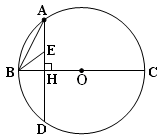
………………………4分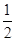 ∠DOB∴∠B=
∠DOB∴∠B=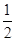 ∠DOB.
∠DOB.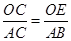 ,从而求得r;(2)由四边形BDEF是平行四边形,得∠DEF=∠B,再由圆周角定理可得,∠B=
,从而求得r;(2)由四边形BDEF是平行四边形,得∠DEF=∠B,再由圆周角定理可得,∠B= 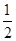 ∠DOB,则△ODE是等边三角形,先得出四边形OFDE是平行四边形.再根据OE=OF,则平行四边形OFDE是菱形.
∠DOB,则△ODE是等边三角形,先得出四边形OFDE是平行四边形.再根据OE=OF,则平行四边形OFDE是菱形.

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源:不详 题型:解答题
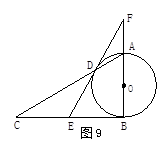
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
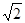 -1,直线l y=-X-
-1,直线l y=-X-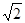 与坐标轴分别交于A,C两点,点B的坐标为(4,1) ,⊙B与X轴相切于点M.
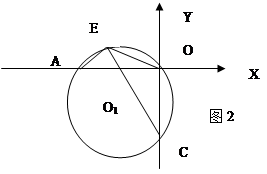
与坐标轴分别交于A,C两点,点B的坐标为(4,1) ,⊙B与X轴相切于点M. 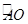 上一点,连接EC,EA.EO,当点E在劣弧
上一点,连接EC,EA.EO,当点E在劣弧 上运动时(不与A,O两点重合),
上运动时(不与A,O两点重合),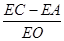 的值是否发生变化?如果不变,求其值,如果变化,说明理由.
的值是否发生变化?如果不变,求其值,如果变化,说明理由. 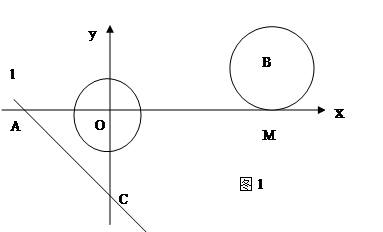 .
. 
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com