
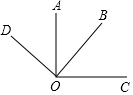
 如图所示,∠AOB=42°,OA⊥OC,OB⊥OD,则∠COD=138°.
如图所示,∠AOB=42°,OA⊥OC,OB⊥OD,则∠COD=138°. 科目:初中数学 来源: 题型:填空题
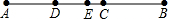 如图,点C为线段AB上一点,若线段AC=12cm,AC=$\frac{3}{2}$BC,D、E两点分别为AC、AB的中点,则DE的长为4cm.
如图,点C为线段AB上一点,若线段AC=12cm,AC=$\frac{3}{2}$BC,D、E两点分别为AC、AB的中点,则DE的长为4cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
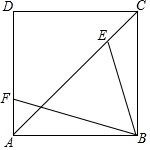 在面积为2的正方ABCD中,EF是线段AC,AD上的动点,且始终保持CE=AF.连接BE,BF.BE+BF是否有最小值?若有,请求出这个值;若无,请说明理由.
在面积为2的正方ABCD中,EF是线段AC,AD上的动点,且始终保持CE=AF.连接BE,BF.BE+BF是否有最小值?若有,请求出这个值;若无,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
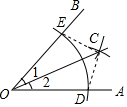 数学课上,小丽用尺规这样作图:(1),以点O为圆心,任意长为半径作弧,交OA,OB于D,E两点;(2)分别以点D,E为圆心,大于$\frac{1}{2}$DE的长为半径作弧,两弧交于点C;(3)作射线OC并连接CD,CE,下列结论不正确的是( )
数学课上,小丽用尺规这样作图:(1),以点O为圆心,任意长为半径作弧,交OA,OB于D,E两点;(2)分别以点D,E为圆心,大于$\frac{1}{2}$DE的长为半径作弧,两弧交于点C;(3)作射线OC并连接CD,CE,下列结论不正确的是( )| A. | ∠1=∠2 | B. | S△OCE=S△OCD | C. | OD=CD | D. | OC垂直平分DE |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC是等腰三角形,AB=AC.
如图,△ABC是等腰三角形,AB=AC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com