
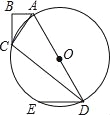
【题目】如图,在四边形ABCD中,AB=6,BC=8,CD=24,AD=26,∠B=90°,以AD为直径作圆O,过点D作DE∥AB交圆O于点E
(1)证明点C在圆O上;
(2)求tan∠CDE的值;
(3)求圆心O到弦ED的距离.
【答案】(1)详见解析;(2)![]() ;(3)圆心O到弦ED的距离为
;(3)圆心O到弦ED的距离为![]() .
.
【解析】
试题分析:(1)如图1,连结CO.先由勾股定理求出AC=10,再利用勾股定理的逆定理证明△ACD是直角三角形,∠C=90°,那么OC为Rt△ACD斜边上的中线,根据直角三角形斜边上的中线等于斜边的一半得出OC=![]() AD=r,即点C在圆O上;(2)如图2,延长BC、DE交于点F,∠BFD=90°.根据同角的余角相等得出∠CDE=∠ACB.在Rt△ABC中,利用正切函数定义求出tan∠ACB=
AD=r,即点C在圆O上;(2)如图2,延长BC、DE交于点F,∠BFD=90°.根据同角的余角相等得出∠CDE=∠ACB.在Rt△ABC中,利用正切函数定义求出tan∠ACB=![]() =
=![]() ,则tan∠CDE=tan∠ACB=
,则tan∠CDE=tan∠ACB=![]() ;(3)如图3,连结AE,作OG⊥ED于点G,则OG∥AE,且OG=
;(3)如图3,连结AE,作OG⊥ED于点G,则OG∥AE,且OG=![]() AE.易证△ABC∽△CFD,根据相似三角形对应边成比例求出CF=
AE.易证△ABC∽△CFD,根据相似三角形对应边成比例求出CF=![]() ,那么BF=BC+CF=
,那么BF=BC+CF=![]() .再证明四边形ABFE是矩形,得出AE=BF=
.再证明四边形ABFE是矩形,得出AE=BF=![]() ,所以OG=
,所以OG=![]() AE=
AE=![]() .
.
试题解析:(1)证明:如图1,连结CO.
∵AB=6,BC=8,∠B=90°,
∴AC=10.
又∵CD=24,AD=26,102+242=262,
∴△ACD是直角三角形,∠C=90°.
∵AD为⊙O的直径,
∴AO=OD,OC为Rt△ACD斜边上的中线,
∴OC=![]() AD=r,
AD=r,
∴点C在圆O上;
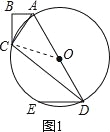
(2)解:如图2,延长BC、DE交于点F,∠BFD=90°.
∵∠BFD=90°,
∴∠CDE+∠FCD=90°,
又∵∠ACD=90°,
∴∠ACB+∠FCD=90°,
∴∠CDE=∠ACB.
在Rt△ABC中,tan∠ACB=![]() =
=![]() ,
,
∴tan∠CDE=tan∠ACB=![]() ;
;
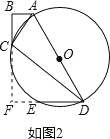
(3)解:如图3,连结AE,作OG⊥ED于点G,则OG∥AE,且OG=![]() AE.
AE.
易证△ABC∽△CFD,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴CF=![]() ,
,
∴BF=BC+CF=8+![]() =
=![]() .
.
∵∠B=∠F=∠AED=90°,
∴四边形ABFE是矩形,
∴AE=BF=![]() ,
,
∴OG=![]() AE=
AE=![]() ,
,
即圆心O到弦ED的距离为![]() .
.
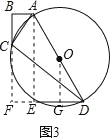


科目:初中数学 来源: 题型:
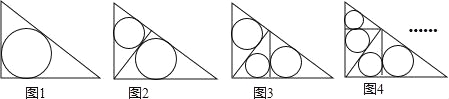
【题目】如图1~4,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依此类推,图10中有10个直角三角形的内切圆,它们的面积分别记为S1,S2,S3,…,S10,则S1+S2+S3+…+S10= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于3x-2x+3y-4xy-5,小糊涂同学说了四句话,其中不正确的是( ).
A. 是一个整式 B. 由4个单项式组成 C. 次数是2 D. 常数项是-5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知线段AB的两个端点分别是A(﹣4,﹣1),B(1,1),将线段AB平移得到线段A′B′,若点A′的坐标为(﹣2,2),则点B′的坐标为( )
A. (3,4) B. (4,3) C. (﹣1,﹣2) D. (﹣2,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富学生的课外活动,拓展孩子们的课外视野,我校的社团活动每年都在增加,社员也一直在增加.2017年我校八年级社员的总人数是300人,2019年我校八年级总校社员有432人。试求出这两年八年级社员人数的平均增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.一个直角三角形一定不是等腰三角形
B.一个钝角三角形一定不是等腰三角形
C.一个等腰三角形一定不是锐角三角形
D.一个等边三角形一定不是钝角三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com