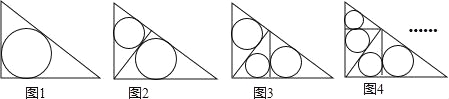
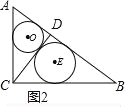
【题目】如图1～4，在直角边分别为3和4的直角三角形中，每多作一条斜边上的高就增加一个三角形的内切圆，依此类推，图10中有10个直角三角形的内切圆，它们的面积分别记为S1，S2，S3，…，S10，则S1+S2+S3+…+S10= ．
【答案】.
【解析】
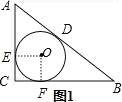
试题分析：（1）如图1，过点O做OE⊥AC，OF⊥BC，垂足为E、F，则∠OEC=∠OFC=90°，∵∠C=90°，∴四边形OECF为矩形.∵OE=OF，∴矩形OECF为正方形.设圆O的半径为r，则OE=OF=r，AD=AE=3﹣r，BD=4﹣r.∴3﹣r+4+r=5，
∴S1=π×12=π； （2）图2，由S△ABC=
，∴CD=
.
在Rt△ACD中：
，∴
.由（1）得：⊙O的半径为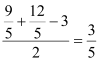
，⊙E的半径为
.∴
.
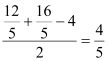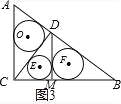
（3）图3，由S△CDB=
，∴
.∴
，
.由（1）得：⊙O的半径=
，：⊙E的半径=
，：⊙F的半径=
.∴S1+S2+S3=π.同理可得S1+S2+S3+S4=.则S1+S2+S3+…+S10=π.
愉快的寒假南京出版社系列答案科目：初中数学 来源： 题型：
【题目】如图1，△ABC是等腰直角三角形，∠BAC＝ 90°，AB＝AC，四边形ADEF是正方形，点B、C分别在边AD、AF上，此时BD＝CF，BD⊥CF成立．
(1)当△ABC绕点A逆时针旋转θ（0°＜θ＜90°）时，如图2，BD＝CF成立吗？若成立，请证明；若不成立，请说明理由．
(2)当△ABC绕点A逆时针旋转45°时，如图3，延长DB交CF于点H.
①求证：BD⊥CF；
②当AB＝2，AD＝3时，求线段DH的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
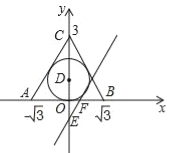
【题目】在平面直角坐标中，△ABC三个顶点坐标为A（﹣
，0）、B（
，0）、C（0，3）．
（1）求△ABC内切圆⊙D的半径．
（2）过点E（0，﹣1）的直线与⊙D相切于点F（点F在第一象限），求直线EF的解析式．
（3）以（2）为条件，P为直线EF上一点，以P为圆心，以2
为半径作⊙P．若⊙P上存在一点到△ABC三个顶点的距离相等，求此时圆心P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
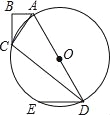
【题目】如图，在四边形ABCD中，AB=6，BC=8，CD=24，AD=26，∠B=90°，以AD为直径作圆O，过点D作DE∥AB交圆O于点E
（1）证明点C在圆O上；
（2）求tan∠CDE的值；
（3）求圆心O到弦ED的距离．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com