
分析 (1)设A种型号家用净水器购进了x台,B种型号家用净水器购进了2x台,C种型号家用净水器购进了(200-3x)台,根据题意列方程即可得到结论;
(2)设每台A型号家用净水器的毛利润是a元,则每台B型号家用净水器的毛利润是2a元,根据保证售完这160台家用净水器的毛利润不低于11000元,列出不等式解答即可;
(3)设A型号家用净水器有x台,则B型号家用净水器有2x台,C型号家用净水器有(n-3x)台,根据题意列方程即可得到结论.
解答 解:(1)设A种型号家用净水器购进了x台,B种型号家用净水器购进了2x台,C种型号家用净水器购进了(200-3x)台,
由题意得150x+200×2x+350×(200-3x)=40000,
解得x=60,
∴2x=120,200-3x=20,
答:A种型号家用净水器购进了60台,B种型号家用净水器购进了120台,C种型号家用净水器购进了20台;
(2)设每台A型号家用净水器的毛利润是a元,则每台B型号家用净水器的毛利润是2a元,
由题意得60a+120×2a+20a≥16000,
解得a≥50,
150+50=200(元).
答:每台A型号家用净水器的售价至少是200元;
(3)解:设A型号家用净水器有x台,则B型号家用净水器有2x台,C型号家用净水器有(n-3x)台,
根据题意得:150x+400x+350(n-3x)=7000,
解得:n=200+$\frac{10}{7}$x,
又∵n-3x≥0,即n≥3x,
∴200+$\frac{10}{7}$x≥3x,
解得:x≤127$\frac{3}{11}$,
由n=200+$\frac{10}{7}$x知x应为7的倍数,
∴x=126,
∴n的最大值为200+$\frac{10}{7}$×126=380.
点评 此题考查一元一次不等式组的实际运用,二元一次方程组的实际运用,找出题目蕴含的数量关系与不等关系是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
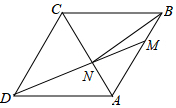 如图,在边长为6的菱形ABCD中,点M在AB边上,DM交AC于点N,连接BN
如图,在边长为6的菱形ABCD中,点M在AB边上,DM交AC于点N,连接BN查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
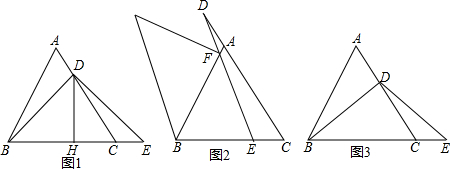
 如图,已知△ABC.
如图,已知△ABC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
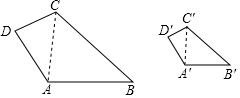 如图,四边形ABCD与四边形A′B′C′D′相似.
如图,四边形ABCD与四边形A′B′C′D′相似.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com