
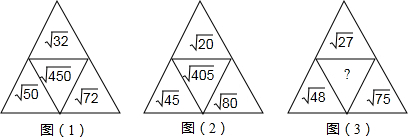
分析 由(1)知$\sqrt{32}$=4$\sqrt{2}$,$\sqrt{50}$=5$\sqrt{2}$,$\sqrt{72}$=6$\sqrt{2}$,$\sqrt{450}$=15$\sqrt{2}$,$\sqrt{32}+\sqrt{50}+\sqrt{72}=\sqrt{450}$;
由(2)知$\sqrt{20}$=2$\sqrt{5}$,$\sqrt{45}$=3$\sqrt{5}$,$\sqrt{80}$=4$\sqrt{5}$,$\sqrt{405}$=2$\sqrt{5}$$+3\sqrt{5}$$+4\sqrt{5}$=9$\sqrt{5}$,
可得:图(3)?=$\sqrt{27}$$+\sqrt{48}$$+\sqrt{75}$,可得结果.
解答 解:∵由(1)知$\sqrt{32}$=4$\sqrt{2}$,$\sqrt{50}$=5$\sqrt{2}$,$\sqrt{72}$=6$\sqrt{2}$,$\sqrt{450}$=15$\sqrt{2}$,$\sqrt{32}+\sqrt{50}+\sqrt{72}=\sqrt{450}$;
由(2)知$\sqrt{20}$=2$\sqrt{5}$,$\sqrt{45}$=3$\sqrt{5}$,$\sqrt{80}$=4$\sqrt{5}$,$\sqrt{405}$=2$\sqrt{5}$$+3\sqrt{5}$$+4\sqrt{5}$=9$\sqrt{5}$,
∴图(3)?=$\sqrt{27}$$+\sqrt{48}$$+\sqrt{75}$=3$\sqrt{3}$$+4\sqrt{3}$$+5\sqrt{3}$=12$\sqrt{3}$=$\sqrt{432}$,
故答案为:$\sqrt{432}$.
点评 本题主要考查了数字的变化规律和算术平方根,根据观察发现规律,运用规律是解答此题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
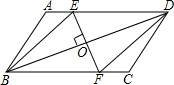 已知ABCD为平行四边形纸片,要想用它剪成一个菱形,小刚说只要过BD中点作BD的垂线交AD、BC于E、F,沿BE、DF剪去两个角,所得的四边形BFDE为菱形.你认为小刚的方法对吗?为什么?
已知ABCD为平行四边形纸片,要想用它剪成一个菱形,小刚说只要过BD中点作BD的垂线交AD、BC于E、F,沿BE、DF剪去两个角,所得的四边形BFDE为菱形.你认为小刚的方法对吗?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
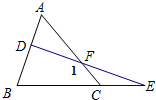 如图,在△ABC中,D为AB边上一点,点E 在BC的延长线上,DE交AC于点F,设∠DFC=∠1,下列关于∠A、∠B、∠E、∠1的关系式中,正确的( )
如图,在△ABC中,D为AB边上一点,点E 在BC的延长线上,DE交AC于点F,设∠DFC=∠1,下列关于∠A、∠B、∠E、∠1的关系式中,正确的( )| A. | ∠A+∠B=∠1+∠E | B. | ∠A+∠B=∠1-∠E | C. | ∠A-∠B=∠1-∠E | D. | ∠A-∠B=∠1+∠E |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
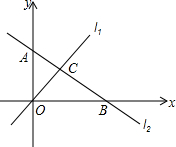 如图,直线l1:y=2x和直线l2:y=kx+b交于C点,A(0,2),B(4,0).
如图,直线l1:y=2x和直线l2:y=kx+b交于C点,A(0,2),B(4,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
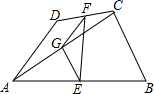 如图,在四边形ABCD中.AD=BC.E,F,G分别是AB,CD,AC的中点,若∠DAC=36°,∠ACB=84°,则∠FEG等于( )
如图,在四边形ABCD中.AD=BC.E,F,G分别是AB,CD,AC的中点,若∠DAC=36°,∠ACB=84°,则∠FEG等于( )| A. | 20° | B. | 24° | C. | 26° | D. | 15° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com